Sine and Cosine Rule with Area of a Triangle
Being equipped with the knowledge of Basic Trigonometry Ratios, we can move one step forward in our quest for studying triangles.
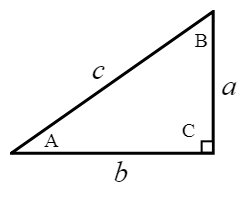
In the case of scalene triangles (triangles with all different lengths), we can use basic trigonometry to find the unknown sides or angles. In principle, each of these scalene triangles can be disassembled into two right-angled triangles.
The resulting derivation from rewriting the unknown height of the triangle in terms of Sine and Cosine functions are the Sine Rule and Cosine Rule.
\(\textrm{Sine Rule (The Law of Sine):}\)
\(\\[1pt]\)
\({\large\frac{{\sin A}}{a} = \frac{{\sin B}}{b} = \frac{{\sin C}}{c}}\)
\(\\[1pt]\)
\(\\[1pt]\)
\(\textrm{Cosine Rule (The Law of Cosine):}\)
\(\\[1pt]\)
\(a^2 = b^2 + c^2 – 2bc\cos A\)
\(\\[1pt]\)
\(b^2 = a^2 + c^2 – 2ac\cos B\)
\(\\[1pt]\)
\(c^2 = a^2 + b^2 – 2ab\cos C\)
\(\\[1pt]\)
As a consequence of the law of sine, we can neatly put a formula for the area of a triangle:
\(\\[1pt]\)
\(\textrm{Area of}\; \triangle ABC = \frac{1}{2}ab\sin C\)
\(\\[1pt]\)
\(\hspace{6.8em} = \frac{1}{2}ac\sin B\)
\(\\[1pt]\)
\(\hspace{6.8em} = \frac{1}{2}bc\sin A\)
\(\\[1pt]\)
As we will soon see in some of the examples below, there are a few things to remember when you are using these formulas:
– Given two sides and an adjacent angle, or two angles and an adjacent side, the triangle can be solved using the Sine Rule.
– Given two sides and an angle in between, or given three sides to find any of the angles, the triangle can be solved using the Cosine Rule.
– Always try to solve the triangle by applying Cosine Rule before Sine Rule due to the ambiguous case with sine rule.
Now let us discuss a little bit deeper about the ambiguous case with sine rule. It arises due to the periodic nature of the sine wave which oscillates between the value of 1 and -1.
To get a clearer picture of what I mean, take a piece of paper and write down the value of \({\small\sin \theta}\) for \({\small \theta =}\) 0 to 180\(^{\circ}\) with an increment of 45\(^{\circ}\).
Sketch the result and you will notice that the sine value of an angle is equal to the sine value of its supplementary angle.
\(\\[1pt]\)
This relationship implies that depending on the ratio of the side length of the triangle, one might have a unique solution or two (an acute triangle, an obtuse triangle or both).
To ensure that you get the correct solution, always check that the equality on the sine rule holds for each pair of the side and the angle.
\(\\[1pt]\)
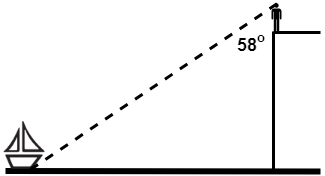
EXAMPLE:
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) \(\angle\)BAC
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) AB
\({\small\hspace{1.2em}\left(c\right).\hspace{0.8em}}\) area of \(\triangle\)ABC
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 2.\enspace}\) \(\triangle\)PQR is a triangle in which PR \(=\) 4.6 cm, QR \(=\) 8 cm and \(\angle\)PRQ \(=\) 39\(^{\circ}\). Find the value of:
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) PQ
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) \(\angle\)QPR
\({\small\hspace{1.2em}\left(c\right).\hspace{0.8em}}\) area of \(\triangle\)PQR
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 3.\enspace}\) In \(\triangle\)XYZ, x \(=\) 9 cm, y \(=\) 10.5 cm and z \(=\) 10 cm . Find the size of the largest angle in the triangle.
\(\\[1pt]\)
\({\small 4.\enspace}\) In a triangle \(\triangle\)ABC with AC \(=\) 7.1 cm, AB \(=\) 4.6 cm and \(\angle\)ACB \(=\) 33\(^{\circ}\). Find the value of \(\angle\)ABC.
\(\\[1pt]\)
\({\small 5.\enspace}\) ABCD is a trapezium. AD is parallel to BC, AD \(=\) 2.5 cm, AB \(=\) 3 cm, BC \(=\) 5 cm and \(\angle\)B \(=\) 73\(^{\circ}\). Calculate CD.
\(\\[1pt]\)
\(\\[1pt]\)
PRACTICE MORE WITH THESE QUESTIONS BELOW!
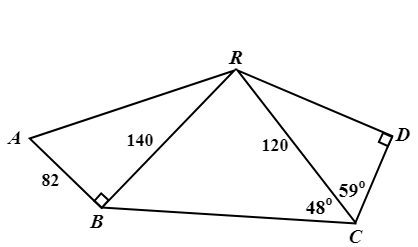
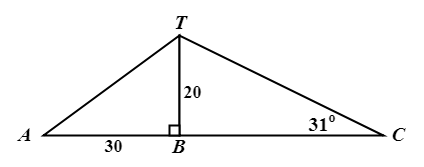
\({\small 1.\enspace}\) Find the missing sides (denoted by small-letter variables) and angles (denoted by capital letters) from each of the triangles below, hence find the area of the triangle.
\(\\[1pt]\)
\(\\[1pt]\)
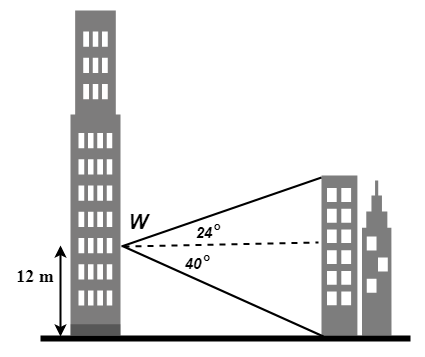
\({\small 2.\enspace}\) A ruined tower is fenced off for safety reasons. To find the height of the tower Rashid stands at a point A and measures the angle of elevation as \({\small 18^{\large{\circ}}}\). He then walks 20 metres directly towards the base of the tower to point B where the angle of elevation is \({\small 31^{\large{\circ}}}\). Calculate the height, h, of the tower.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 3.\enspace}\) ABCD is a quadrilateral. \({\small AB = 7 \ \textrm{cm}, \ AD = 6 \ \textrm{cm} \ \textrm{and} \ BC = 9 \ \textrm{cm}}\). Angle ABC \(= \ {\small 75^{\large{\circ}}}\) and angle ADC \(= \ {\small 90^{\large{\circ}}}\). Calculate the perimeter of ABCD.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 4.\enspace}\) The side of a regular pentagon is 24 cm long. Approximate the radius of the circumscribed circle. (Hint: use Sine Rule).
\({\small 5.\enspace}\) TAC is a triangle. Point B is located along the straight line AC. TB \(=\) 18 cm and TC \(=\) 12 cm. \({\small \angle }\) ATB \( = {\small 61^{\large{\circ}}}\) and \({\small \angle }\) BTC \(= {\small 27^{\large{\circ}}}\). Calculate
\({\small\hspace{1.2em}\left(a\right).\enspace \angle }\) TCB
\({\small\hspace{1.2em}\left(b\right).\enspace}\) TA.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 6.\enspace}\) In the figure, AB \(=\) 3 cm, BC \(=\) 6 cm, CA \(=\) 7 cm, AD \(=\) 8 cm and DC \(=\) 4 cm. Calculate the length of BD.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 7.\enspace}\) In the diagram, BCD is a straight line. BC \(=\) 36 cm, CD \(=\) 24 cm and the area of \({\small \triangle {ACD} \ = \ 178 \ \mathrm{{cm}^{2}}}\). Calculate the area of \({\small \triangle {ABC}}\).
\(\\[1pt]\)
\(\\[1pt]\)
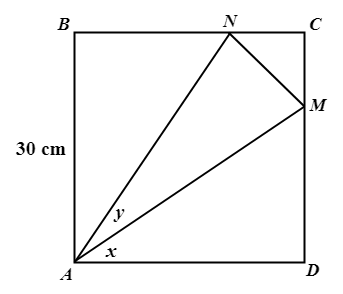
\({\small 8.\enspace}\) Given in the figure, AQ \(=\) 15 cm, QB \(=\) 6.7 cm, AP \(=\) 5.5 cm, PC \(=\) 10.4 cm and \({\small \angle }\) BAC \( = {\small 74^{\large{\circ}}}\). Calculate the area of the quadrilateral PQBC and the length of BC.
\(\\[1pt]\)
\(\\[1pt]\)
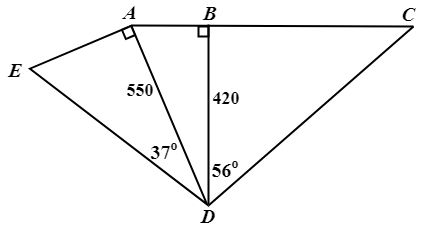
\({\small 9.\enspace}\) The area of \({\small \triangle {ABD} \ = \ 33.6 \ \mathrm{{m}^{2}}}\). Find the length of CD.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 10.\enspace}\) Jane and Peter are considering buying a block of land. The land agent supplies them with the given accurate sketch. Find the area of the property.
\(\\[1pt]\)
As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .