Basic Trigonometry

Basic Trigonometry

Trigonometry is another big topic in Mathematics. It is the study of measuring triangles, the most basic two-dimensional figure. It has practical application in many areas such as architecture, geometry, physics and others since more complex shapes are just collections of triangles as the building blocks.

To become proficient in trigonometry, a strong knowledge of the Pythagorean Theorem and the right-angled triangle are pivotal. To begin with, the three basic trigonometric functions are described as follows:

\(\\[10pt]\quad{\small 1.\quad}\)\( \sin \theta = \large{\frac{opp}{hyp}}\)
Sine of an angle \(({\small\sin \theta})\) is the ratio of the opposite side (opp) to the hypotenuse (hyp) of a right-angled triangle.

\(\\[10pt]\quad{\small 2.\quad}\)\( \cos \theta = \large{\frac{adj}{hyp}}\)
Cosine of an angle \(({\small\cos \theta})\) is the ratio of the adjacent side (adj) to the hypotenuse (hyp) of a right-angled triangle.

\(\\[10pt]\quad{\small 3.\quad}\)\( \tan \theta = \large{\frac{opp}{adj}}\)
Tangent of an angle \(({\small\tan \theta})\) is the ratio of the opposite side (opp) to the adjacent (adj) of a right-angled triangle.

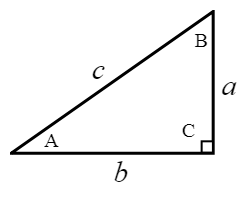
Generally, small letters (a, b, c, …) are used to represent sides of a triangle and capital letters (A, B, C, …) are used to represent the angle on the opposite side of a triangle side. Please take a look at the illustration below for a clearer usage and notations.
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[15pt]\quad \sin A = \large{\frac{opp}{hyp}=\frac{a}{c}},\)\(\quad \sin B = \large{\frac{opp}{hyp}=\frac{b}{c}}\)
\(\\[15pt]\quad \cos A = \large{\frac{adj}{hyp}=\frac{b}{c}},\)\(\quad \cos B = \large{\frac{adj}{hyp}=\frac{a}{c}}\)
\(\\[15pt]\quad \tan A = \large{\frac{opp}{adj}=\frac{a}{b}},\)\(\quad \tan B = \large{\frac{opp}{adj}=\frac{b}{a}}\)
\(\\[5pt]\)
Use the acronym “SOH”, “CAH”, “TOA” to help you remember these formulas.

Try the exercises below and if you need any help, just look at the solution I have written. Cheers ! =) .
\(\\[1pt]\)

EXAMPLE:

\({\small 1.\enspace}\) For each of the following right-angled triangles, state the value of:
\({\small\hspace{1.2em}\left(i\right).\hspace{0.8em}}\) \({\small\sin X},\quad{\small\hspace{1.2em}\left(iv\right).\hspace{0.5em}}\) \({\small\sin Y}\),
\({\small\hspace{1.2em}\left(ii\right).\hspace{0.5em}}\) \({\small\cos X},\quad{\small\hspace{1.2em}\left(v\right).\hspace{0.7em}}\) \({\small\cos Y}\),
\({\small\hspace{1.2em}\left(iii\right).\hspace{0.2em}}\) \({\small\tan X},\quad{\small\hspace{1em}\left(vi\right).\hspace{0.5em}}\) \({\small\tan Y}\).
\(\\[1pt]\)

Show solution:

\(\\[10pt]{\small\hspace{1.2em}(a).\enspace(i).\hspace{0.8em}\sin X} = \frac{8 \, \mathrm{cm}}{10 \, \mathrm{cm}}=\frac{4}{5}\)
\(\\[10 pt]{\small\hspace{3.1em}\left(ii\right).\hspace{0.4em}\cos X} = \frac{6 \, \mathrm{cm}}{10 \, \mathrm{cm}}=\frac{3}{5}\)
\(\\[10pt]{\small\hspace{3.1em}\left(iii\right).\hspace{0.1em}\tan X} = \frac{8 \, \mathrm{cm}}{6 \, \mathrm{cm}}=\frac{4}{3}\)
\(\\[10pt]{\small\hspace{3.1em}\left(iv\right).\hspace{0.5em}\sin Y} = \frac{6 \, \mathrm{cm}}{10 \, \mathrm{cm}}=\frac{3}{5}\)
\(\\[10pt]{\small\hspace{3.1em}\left(v\right).\hspace{0.6em}\cos Y} = \frac{8 \, \mathrm{cm}}{10 \, \mathrm{cm}}=\frac{4}{5}\)
\(\\[10pt]{\small\hspace{3.1em}\left(vi\right).\hspace{0.3em}\tan Y} = \frac{6 \, \mathrm{cm}}{8 \, \mathrm{cm}}=\frac{3}{4}\)
\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.2em}(b).\enspace(i).\hspace{0.8em}\sin X} = \frac{8 \, \mathrm{cm}}{10 \, \mathrm{cm}}=\frac{4}{5}\)
\(\\[10pt]{\small\hspace{3.1em}\left(ii\right).\hspace{0.4em}\cos X} = \frac{6 \, \mathrm{cm}}{10 \, \mathrm{cm}}=\frac{3}{5}\)
\(\\[10pt]{\small\hspace{3.1em}\left(iii\right).\hspace{0.1em}\tan X} = \frac{8 \, \mathrm{cm}}{6 \, \mathrm{cm}}=\frac{4}{3}\)
\(\\[10pt]{\small\hspace{3.1em}\left(iv\right).\hspace{0.5em}\sin Y} = \frac{6 \, \mathrm{cm}}{10 \, \mathrm{cm}}=\frac{3}{5}\)
\(\\[10pt]{\small\hspace{3.1em}\left(v\right).\hspace{0.6em}\cos Y} = \frac{8 \, \mathrm{cm}}{10 \, \mathrm{cm}}=\frac{4}{5}\)
\(\\[10pt]{\small\hspace{3.1em}\left(vi\right).\hspace{0.3em}\tan Y} = \frac{6 \, \mathrm{cm}}{8 \, \mathrm{cm}}=\frac{3}{4}\)
\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.2em}(c).\enspace(i).\hspace{0.8em}\sin X} = \frac{b}{c}\)
\(\\[10pt]{\small\hspace{3.1em}\left(ii\right).\hspace{0.4em}\cos X} = \frac{a}{c}\)
\(\\[10pt]{\small\hspace{3.1em}\left(iii\right).\hspace{0.1em}\tan X} = \frac{b}{a}\)
\(\\[10pt]{\small\hspace{3.1em}\left(iv\right).\hspace{0.5em}\sin Y} = \frac{a}{c}\)
\(\\[10pt]{\small\hspace{3.1em}\left(v\right).\hspace{0.6em}\cos Y} = \frac{b}{c}\)
\(\\[10pt]{\small\hspace{3.1em}\left(vi\right).\hspace{0.3em}\tan Y} = \frac{a}{b}\)
\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.2em}(d).\enspace(i).\hspace{0.8em}\sin X} = \frac{q}{p}\)
\(\\[10pt]{\small\hspace{3.1em}\left(ii\right).\hspace{0.4em}\cos X} = \frac{r}{p}\)
\(\\[10pt]{\small\hspace{3.1em}\left(iii\right).\hspace{0.1em}\tan X} = \frac{q}{r}\)
\(\\[10pt]{\small\hspace{3.1em}\left(iv\right).\hspace{0.5em}\sin Y} = \frac{r}{p}\)
\(\\[10pt]{\small\hspace{3.1em}\left(v\right).\hspace{0.6em}\cos Y} = \frac{q}{p}\)
\(\\[10pt]{\small\hspace{3.1em}\left(vi\right).\hspace{0.3em}\tan Y} = \frac{r}{q}\)

\(\\[1pt]\)
\({\small 2.\enspace}\) Find the value of the unknowns in each of the following right-angled triangles.
\(\\[1pt]\)

Show solution:

\(\\[7pt]{\small\hspace{1.2em}\left(a\right).\enspace} \sin 34^{\circ} = {\large\frac{a}{15}}\)
\(\\[5pt]{\small\hspace{5.6em}} a = \sin 34^{\circ} \times 15\)
\(\\[7pt]{\small\hspace{6.2em}} \approx 8.39\)
\(\\[10pt]\hspace{3.3em} \cos 34^{\circ} = {\large\frac{b}{15}}\)
\(\\[5pt]{\small\hspace{5.8em}} b = \cos 34^{\circ} \times 15\)
\({\small\hspace{6.2em}} \approx 12.44\)
\(\\[1pt]\)
\(\\[7pt]{\small\hspace{1.2em}\left(b\right).\enspace} \tan 64^{\circ} = {\large\frac{c}{12}}\)
\(\\[5pt]{\small\hspace{5.8em}} c = \tan 64^{\circ} \times 12\)
\(\\[10pt]{\small\hspace{6.2em}} \approx 24.60\)
\(\\[10pt]\hspace{3.3em} \cos 64^{\circ} = {\large\frac{12}{d}}\)
\(\\[10pt]{\small\hspace{5.7em}} d = {\large\frac{12}{\cos 64^{\circ}}}\)
\({\small\hspace{6.2em}} \approx 27.37\)
\(\\[1pt]\)
\(\\[7pt]{\small\hspace{1.2em}\left(c\right).\enspace} \tan 52^{\circ} = {\large\frac{7.5}{e}}\)
\(\\[10pt]{\small\hspace{5.8em}} e = {\large\frac{7.5}{\tan 62^{\circ}}}\)
\(\\[10pt]{\small\hspace{6.2em}} \approx 5.86\)
\(\\[10pt]\hspace{3.3em} \sin 52^{\circ} = {\large\frac{7.5}{f}}\)
\(\\[10pt]{\small\hspace{5.6em}} f = {\large\frac{7.5}{\sin 52^{\circ}}}\)
\({\small\hspace{6.1em}} \approx 9.52\)
\(\\[1pt]\)
\(\\[7pt]{\small\hspace{1.2em}\left(d\right).\hspace{1em}} \cos\: c\: = {\large\frac{24.3}{35.7}}\)
\(\\[10pt]{\small\hspace{5.8em}} c = \cos^{-1}({\large\frac{24.3}{35.7}})\)
\(\\[10pt]{\small\hspace{6.2em}} \approx 47.1^{\circ}\)
* Note that to find an angle, use the inverse trigonometric function such as the inverse cosine \((\cos^{-1})\) in this question
\(\\[1pt]\)
\(\\[10pt]\hspace{3.3em} \sin 47.1^{\circ} = {\large\frac{d}{35.7}}\)
\(\\[10pt]{\small\hspace{6.4em}} d = 35.7 \times \sin 47.1^{\circ}\)
\({\small\hspace{6.9em}} \approx 26.15\)

\(\\[1pt]\)
\({\small 3.\enspace}\) A point P on level ground is 43 m away from the top of a vertical post QR of height 32 m. Find \(\angle\)QPR.
\(\\[1pt]\)

Show solution:

\(\\[10pt]\hspace{1.2em} \tan\:\angle\, QPR = {\large\frac{32\, \mathrm{m}}{43\, \mathrm{m} }}\)
\(\\[10pt]\hspace{3em} \angle\, QPR = \tan^{-1}({\large\frac{32}{43}})\)
\(\\[10pt]\hspace{6.5em} \approx 36.7^{\circ}\)

\(\\[1pt]\)
\({\small 4.\enspace}\) To travel from school to his home, Ethan can walk along the straight path SH. However, he sometimes take a detour by travelling from school to the food centre F, then from the food centre to his home. Find
\({\small\hspace{1.2em}\left(a\right).\enspace}\)SF, the distance between the school and the food centre,
\({\small\hspace{1.2em}\left(b\right).\enspace}\)FH, the distance between the food centre and his home.

Show solution:

\(\\[10pt]{\small\hspace{1.2em}\left(a\right).\enspace} \sin 21.6^{{\large \circ}} = \ {\large\frac{SF}{86.5\, \mathrm{m} }}\)
\(\\[10pt]{\small\hspace{5.7em} SF \ = \ \sin 21.6^{{\large \circ}} \times 86.5\, \mathrm{m}}\)
\(\\[5pt]{\small\hspace{7.3em} \approx \ 31.84\,\mathrm{m}} \)
\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.2em}\left(b\right).\enspace} \cos 21.6^{{\large \circ}} = \ {\large\frac{FH}{86.5\, \mathrm{m} }}\)
\(\\[10pt]{\small\hspace{5.5em} FH \ = \ \cos 21.6^{{\large \circ}} \times 86.5\, \mathrm{m}}\)
\({\small\hspace{7.3em} \approx \ 80.43\,\mathrm{m}} \)

\(\\[1pt]\)
\({\small 5.\enspace}\) In a computer game, a soldier stands on the top of an observatory AB 45 m above the ground. He observes the enemy at the point E. Given that \(\angle\)AEB \({\small= 38^{\circ}}\), find the distance between the enemy and the foot of the observatory.

Show solution:

\(\\[10pt]\hspace{1.2em} \tan 38^{\circ} = {\large\frac{45\, \mathrm{m}}{BE}}\)
\(\\[10pt]\hspace{2.7em} BE = {\large\frac{45\, \mathrm{m}}{\tan 38^{\circ}}}\)
\(\\[10pt]\hspace{4.5em} \approx 57.60\, \mathrm{m} \)

\(\\[1pt]\)

PRACTICE AND TRY THESE QUESTIONS BELOW!

\({\small 1.\enspace}\) Triangle ABC is a right-angled triangle. Find
\({\small\hspace{1.2em}\left(a\right).\enspace \cos A}\)
\({\small\hspace{1.2em}\left(b\right).\enspace \tan A}\)
\({\small\hspace{1.2em}\left(c\right).\enspace \sin C}\)

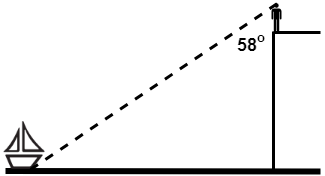
\({\small 2.\enspace}\) A man at the top of a vertical cliff observes a boat at the sea. State the angle of depression of the boat from the man.

\(\\[1pt]\)

\({\small 3.\enspace}\) The angle of elevation of the top of a building from a point on the ground 220 m away from the foot of the building is 16\(^{\circ}\). What is the height of the building?

\({\small 4.\enspace}\) A boy standing in the middle of two flagpoles 78 m apart finds that the angle of elevation of the tops of the flagpoles from the point where he is standing are 34\(^{\circ}\) and 43\(^{\circ}\). Find the difference in the heights of the two flagpoles.

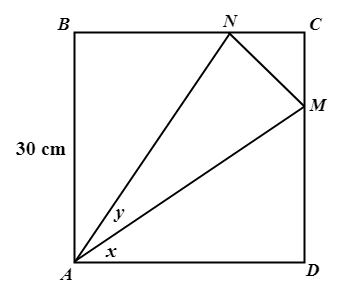
\({\small 5.\enspace}\) In the diagram, ABCD is a square of side 30 cm, CM : MD \(=\) 1 : 2 and \(\angle\)MDA \(=\) \(\angle\)MCN.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Find the exact value of \({\small\tan X}\).
\({\small\hspace{1.2em}\left(b\right).\enspace}\) Find the length of CN.
\({\small\hspace{1.2em}\left(c\right).\enspace}\) Calculate the value of y.

\(\\[1pt]\)

\({\small 6.\enspace}\) If x is an acute angle and \({\small\sin x} = \large{\frac{15}{17}}\), find the exact value of \({\small\cos x}\) and \({\small\tan x}\).

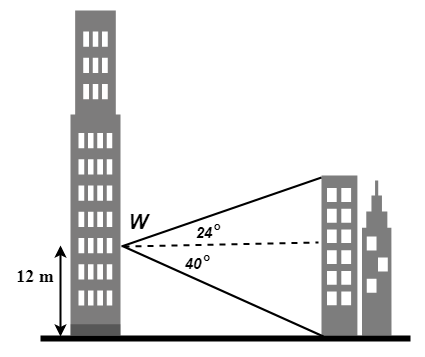
\({\small 7.\enspace}\) From the window, W of a building which is 12 m above the ground level, a man observes that the angle of elevation of the top, A of another building is 24\(^{\circ}\) and the angle of depression of its foot, B is 40\(^{\circ}\). Find the height of the second building.

\(\\[1pt]\)

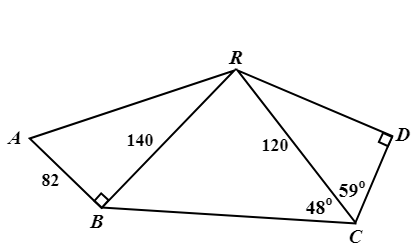
\({\small 8.\enspace}\) The diagram shows footpaths BR and CR in a park ABCDR. BR \(=\) 140 m, CR \(=\) 120 m and AB \(=\) 82 m. \(\angle\)BCR \(=\) 48\(^{\circ}\), \(\angle\)DCR \(=\) 59\(^{\circ}\) and \(\angle\)ABR \(=\) \(\angle\)CDR \(=\) 90\(^{\circ}\). Calculate
\({\small\hspace{1.2em}\left(a\right).\enspace}\) CD,
\({\small\hspace{1.2em}\left(b\right).\enspace}\) \(\angle\)ARB.

\(\\[1pt]\)

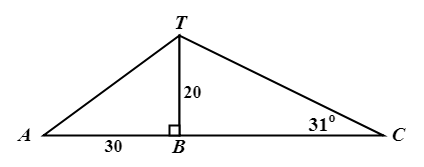
\({\small 9.\enspace}\) A, B and C are three points on horizontal ground. BT is a vertical mast of height 20 m. The top of the mast is joined to A and C by straight wires. \(\angle\)BCT \(=\) 31\(^{\circ}\).
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Calculate the length of the wire CT.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) Given that AB is 30 m, calculate the angle of elevation of T from A.

\(\\[1pt]\)

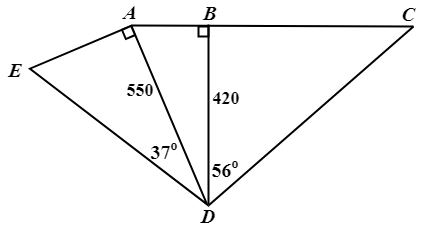
\({\small 10.\enspace}\) The diagram shows the available paths in a park. ABC is a straight line. \(\angle\)EAD \(=\) \(\angle\)ABD \(=\) 90\(^{\circ}\), \(\angle\)ADE \(=\) 37\(^{\circ}\) and \(\angle\)BDC \(=\) 56\(^{\circ}\). BD \(=\) 420 m and AD \(=\) 550 m. Calculate
\({\small\hspace{1.2em}\left(a\right).\enspace}\) AB,
\({\small\hspace{1.2em}\left(b\right).\enspace}\) BC,
\({\small\hspace{1.2em}\left(c\right).\enspace}\) DE.
\(\\[1pt]\)

As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .