I have compiled some of the challenging questions I have covered with my students. For those who are interested, you are more than welcomed to give the questions below a try! Cheers =) .
\(\\[1pt]\)
\({\small 1.\enspace}\) Given that:
\(\\[1pt]\)
\({\LARGE\frac{108}{17} \ = \ } {\LARGE a} + \huge{\frac{1}{b \ + \ \frac{1}{c \ + \ \frac{1}{d \ + \ 2}}}}\)
\(\\[1pt]\)
with
a,
b,
c and
d are positive integers. Find the value of:
\(\\[1pt]\)
\({\LARGE\frac{a^3 \ – \ 3a^2b \ + \ 3ab^2 \ – \ b^3}{c^3 \ – \ 3c^2d \ + \ 3cd^2 \ – \ d^3}} \)
To get the value of a, b, c and d, we’ll need to convert the simple fraction into a mixed fraction.
\(\\[1pt]\)
The whole number in the mixed fraction has to be the largest possible value to ensure the fraction part in the mixed fraction always has a numerator that is smaller than the denominator.
\(\\[1pt]\)
\(\\[10pt]\)By using contradiction,
\(\\[15pt]\frac{p}{q} \ = \ \frac{p/p}{q/p} \ = \ \frac{1}{q/p} \)
If \(\\[10pt]\; \frac{p}{q} \ >\ 1 \;\) then \(\; \frac{q}{p} \lt 1\)
There are no value of a, b, c and d possible as positive integers.
\(\\[1pt]\)
\(\\[10pt]{\large \frac{108}{17}} \ = \ 6 + {\large \frac{6}{17}}\)
\(\hspace{1.2em} a \ = \ 6 \)
\(\\[1pt]\)
\(\\[15pt]{\large\frac{6}{17}} \ = \ {\large \frac{6/6}{17/6} \ =\ \frac{1}{17/6}}\)
\(\\[10pt]{\large\frac{17}{6}} \ = \ 2 + {\large\frac{5}{6}}\)
\(\hspace{1.2em} b \ = \ 2\)
\(\\[1pt]\)
\(\\[15pt]{\large\frac{5}{6}} \ = \ {\large \frac{5/5}{6/5} \ =\ \frac{1}{6/5}}\)
\(\\[10pt]{\large\frac{6}{5}} \ = \ 1 + {\large\frac{1}{5}}\)
\(\hspace{1.2em} c \ = \ 1\)
\(\\[1pt]\)
\(\\[7pt]\ 5 \ = \ d \ + \ 2\)
\(\hspace{1.2em} d \ = \ 3\)
\(\\[1pt]\)
We’ll then factorize the expression and substitute each value of a, b, c and d.
\(\\[1pt]\)
\(\\[18pt]{\Large\frac{a^3 \ – \ 3a^2b \ + \ 3ab^2 \ – \ b^3}{c^3 \ – \ 3c^2d \ + \ 3cd^2 \ – \ d^3}} = {\large\frac{(a\ -\ b)^3}{(c\ -\ d)^3}} \)
\(\\[15pt]\ = \ {\large {(\frac{a\ -\ b}{c\ -\ d})}^{3}} \ = \ {\large {(\frac{6\ -\ 2}{1\ – \ 3})}^{3} }\)
\(\ = \ {(-2)}^{3} \ = \ -8\)
\(\\[1pt]\)
\({\small 2.\enspace}\) One year, 23 September was a Monday. What day of the week was 10 November that year?
\(\hspace{1.2em}\)(a). Sunday
\(\hspace{1.2em}\)(b). Monday
\(\hspace{1.2em}\)(c). Thursday
\(\hspace{1.2em}\)(d). Saturday
There is a total of 17 days from 23 Sept to 10 Nov. Since there are 7 days in a week, every multiple of 7 days will reset to another Mondays. The reminder gives us 3 days and hence, the answer is 3 days after a Monday which is Thursday (c).
\(\\[1pt]\)
\({\small 3.\enspace}\) In a rectangle
ABCD, point
F and
E are located at the side
AB and
DC in such a way a rhombus
BFDE is formed, as shown in the picture.
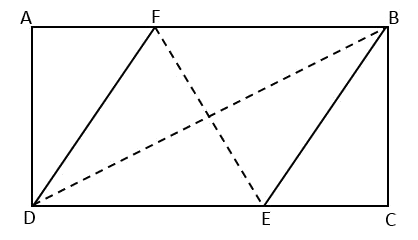
If
AB \(=\) 6.4 cm and
BC \(=\) 4.8 cm, find
EF.
Let the side of the rhombus
BFDE \(= x\).
We can solve the value of \( x\) by using Pythagoras Theorem on the right-angled triangle \(\triangle {\small BCE}\).
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[7pt]\hspace{2.1em} {BE}^2 \ = \ {BC}^2 \ + \ {CE}^2\)
\(\\[7pt]{\small\hspace{3.1em}} x^2 \ = \ (6.4 \ – \ x)^2 \ + \ {4.8}^2\)
\(\\[7pt]{\small\hspace{3.1em}} x^2 \ = \ 40.96 \ – \ 12.8x \ + \ x^2 \ + \ 23.04 \)
\(\\[7pt]{\small\hspace{1.8em}} 12.8x \ = \ 64 \)
\(\\[15pt]{\small\hspace{3.6em}} x \ = \ 5 \ \mathrm{cm} \)
Finally, we can solve
EF by using Pythagoras Theorem again on the triangle \(\triangle {\small DFE}\). We will draw an additional point
M along the side
DE whereby the length
DM is the height of the triangle \(\triangle {\small DFE}\).
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[7pt]\hspace{2.1em} {EF}^2 \ = \ {FM}^2 \ + \ {ME}^2\)
\(\\[7pt]{\small\hspace{2.1em}} {EF}^2 \ = \ {4.8}^2 \ + \ {3.6}^2\)
\(\\[7pt]{\small\hspace{2.1em}} {EF}^2 \ = \ 23.04 \ + \ 12.96 \)
\(\\[7pt]{\small\hspace{2.6em}} EF \ = \sqrt {36} \)
\({\small\hspace{2.6em}} EF \ = \ 6 \ \mathrm{cm}\)
\(\\[1pt]\)
\({\small 4.\enspace}\) Given that: \((3x\:+\:4y \:-\: 5z)^{3}\), find the sum of coefficients of the terms: \(x^2y,\:y^2z\) and \(x^2z\).
We will find the formula for the general cube of difference and then apply it to the question.
\(\\[1pt]\)
\(\\[7pt] {\small (a \ – \ b)^{3} \ = \ (a \ – \ b)^{2} \ (a \ – \ b) }\)
\(\\[7pt]\hspace{3em} {\small = \ (a^2 \ – 2ab \ + \ b^2) \ (a \ – \ b) }\)
\(\\[7pt]\hspace{3em} {\small = \ a^3 \ – a^2b \ – \ 2a^2b \ + \ 2ab^2 \ + \ ab^2 \ – \ b^3 }\)
\(\\[7pt]\hspace{3em} {\small = \ a^3 \ – 3a^2b \ + \ 3ab^2 \ – \ b^3 }\)
\(\\[15pt]\hspace{3em} {\small = \ a^3 \ – 3ab \ (a \ – \ b) \ – \ b^3 }\)
Let’s apply the above formula to the question.
\(\\[1pt]\)
\(\\[15pt] {\small (3x\:+\:4y \:-\: 5z)^{3} \ = [(3x\:+\:4y) \:-\: 5z]^{3} }\)
\(\\[7pt] {\small (a \ – \ b)^{3} \ = \ a^3 \ – 3ab \ (a \ – \ b) \ – \ b^3 }\)
\(\\[7pt] \hspace{1.2em} * {\ \small (3x \ + \ 4y) \ = \ a \; }\) and \(\;{\small 5z \ = \ b }\)
\(\\[15pt] {\small = \ (3x+4y)^{3}-3(3x+4y)(5z)(3x+4y-5z)-(5z)^{3} }\)
\(\\[7pt] \hspace{1.2em} * {\ \small (3x+4y)^{3} }\)
\(\\[7pt] \hspace{1.2em} {\small = (3x)^{3}+3(3x)(4y)(3x+4y)+(4y)^{3} }\)
\(\\[15pt] \hspace{1.2em} {\small = 27x^3+108x^2y+144xy^2+64y^3 }\)
\(\\[7pt] \hspace{1.2em} * {\ \small -3(3x+4y)(5z)(3x+4y-5z) }\)
\(\\[7pt] \hspace{1.2em} {\small = -15z(3x+4y)(3x+4y-5z) }\)
\(\\[15pt] \hspace{1.2em} {\small = -135x^2z-360xyz+225xz^2-240y^2z+300yz^2}\)
\(\\[7pt] \hspace{1.2em} * {\ \small -(5z)^3 }\)
\(\\[15pt] \hspace{1.2em} {\small = -125z^3}\)
We’ll add up the coefficients of \(x^2y,\:y^2z\) and \(x^2z\) to get the final answer:
\(\\[7pt]{\small = \ 108 \ – \ 240 \ – \ 135 }\)
\( = \ -267\)
\(\\[1pt]\)
\({\small 5.\enspace}\) Find the result of:
\(\\[1pt]\)
\({\large\frac{5}{(2 \ \times \ 3)^{2}}}+{\large\frac{7}{(3 \ \times \ 4)^{2}}}+{\large\frac{9}{(4 \ \times\ 5)^{2}}} + \dots + {\large\frac{23}{(11 \ \times \ 12)^{2}}}\)
Firstly, we can find the sum pattern of these fractions. If you look closely, you will find that the numerator is simply the addition of two consecutive numbers while the denominator is the square multiplication of that same two consecutive numbers in the numerator.
\(\\[1pt]\)
With that in mind, let’s write the question in mathematical notations for summation and number pattern. The above summation can be written as follows:
\(\\[1pt]\)
\(\displaystyle \sum_{n=2}^{11} \frac{n \ + \ (n+1)}{[n \ (n \ + \ 1)]^{2}} \ = \ \sum_{n=2}^{11} \frac{2n+1}{n^2 \ (n \ + \ 1)^{2}}\)
\(\\[1pt]\)
Next we will prove that the above form can be represented as the difference between two fractions, \({\large \frac{1}{n^2} }\) and \({\large \frac{1}{(n \ + \ 1)^2} }\).
\(\\[1pt]\)
\(\\[17pt] \hspace{1.2em} {\large \frac{1}{n^2} \ – \ \frac{1}{(n \ + \ 1)^2} }\)
\(\\[17pt] \hspace{1.2em} { = \ \large \frac{(n \ + \ 1)^2}{n^2 \ (n \ + \ 1)^2} \ – \ \frac{n^2}{n^2 \ (n+1)^2} }\)
\(\\[17pt] \hspace{1.2em} { = \ \large \frac{n^2 \ + \ 2n \ + \ 1 \ – \ n^2}{n^2 \ (n \ + \ 1)^2} }\)
\( \hspace{1.2em} { = \ \large \frac{2n \ + \ 1}{n^2 \ (n \ + \ 1)^2} }\) (proven.)
\(\\[1pt]\)
So, we’ll rewrite the above summation as follows:
\(\\[1pt]\)
\(\\[20pt]\displaystyle \sum_{n=2}^{11} \frac{n \ + \ (n+1)}{[n \ (n \ + \ 1)]^{2}} \ = \ \sum_{n=2}^{11} \bigg[\frac {1}{n^2} \ – \ \frac{1}{(n \ + \ 1)^2}\bigg]\)
\(\\[25pt]= {\large \frac{1}{2^2}} – {\large \frac{1}{3^2}} + {\large \frac{1}{3^2}} – {\large \frac{1}{4^2}} + \dotsc – \dotsc + {\large \frac{1}{11^2}} – {\large \frac{1}{12^2}}\)
Each of the terms cancel each other except for the first term and the last term only, leaving behind:
\(\\[1pt]\)
\(\\[15pt] \hspace{1.2em} = {\large \frac{1}{2^2}} \ – \ {\large \frac{1}{12^2}}\)
\(\\[15pt] \hspace{1.2em} = {\large \frac{1}{4}} \ – \ {\large \frac{1}{144}}\)
\( \hspace{1.2em} = {\large \frac{35}{144}} \)
\(\\[1pt]\)
\({\small 6.\enspace}\) Mr. Santoso has five kids. Each of them is given a different amount of pocket money per week. Adi gets half of what Edi receives, Beni gets $1 more from Adi, Citra gets $1.5 more than Adi and Doni gets $1.7 less that Edi. If the average of their pocket money is $5.2 in a week, what is the amount of pocket money that Doni received in a year?
Let the amount of money that Adi receives \(= {\small x }\)
Edi receives \(= {\small 2x }\)
Beni receives \(= {\small x \ + \ 1 } \)
Citra receives \(= {\small x \ + \ 1.5 }\)
Doni receives \(= {\small 2x \ – \ 1.7 }\)
\(\\[1pt]\)
\( \\[7pt] {\small x + 2x + x + 1 + x + 1.5 + 2x \ – \ 1.7 \ } = \ {\small 5.2 \times 5 }\)
\( \\[7pt] \hspace{1.2em} {\small 7x + 0.8 \ = \ 26 }\)
\( \\[7pt] \hspace{3.3em} {\small 7x \ = \ 25.2 }\)
\( \\[15pt] \hspace{3.7em} {\small x \ = \ 3.6 }\)
Doni receives in a year:
\( \\[7pt]\hspace{1.2em} = {\small (2 \times 3.6 \ – \ 1.7) \ \times \ 52 }\)
\( \hspace{1.2em} = {\small $ \ 286}\)
\(\\[1pt]\)
\({\small 7.\enspace}\) The same rule is applied to the top number in each box to give the bottom number.
\(\\[1pt]\)

\(\\[1pt]\)
What number must box
x be ?
(a). 30
(b). 32
(c). 34
(d). 40
The pattern is: multiply the top number in the box by 3 and then add up the result with 4.
Hence, the answer is: \( {\small \ 10 \times 3 \ + \ 4 \ = \ 34 \ (c).} \)
\(\\[1pt]\)
\({\small 8.\enspace}\) Oscar, Lily and Jack collect souvenir coins. Oscar has 44 more coins than Lily and 48 more coins than Jack. Oscar has 6 more coins than Lily and Jack combined. How many coins do Oscar, Lily and Jack have altogether?
(a). 196
(b). 166
(c). 156
(d). 146
Let Oscar has \(= {\small x }\) coins
\(\hspace{2em}\) Lily has \(= {\small (x \ – \ 44)}\) coins
\(\hspace{1.8em}\) Jack has \(= {\small (x \ – \ 48)}\) coins
\(\\[1pt]\)
\( \\[7pt] \hspace{2.7em} {\small x \ – \ 6 \ = \ x \ – \ 44 \ + \ x \ – \ 48 }\)
\( \\[7pt] \hspace{1.2em} {\small x \ – \ x \ – \ x \ = \ -44 \ -48 \ + \ 6 }\)
\( \\[15pt] \hspace{4.1em} {\small x \ = \ 86 }\)
\( \\[7pt]\) Altogether, they have:
\( \\[7pt]\hspace{1.2em} = \ {\small 86 + 86 \ – \ 44 + 86 \ – \ 48}\)
\( \hspace{1.2em} = \ \)166 coins (b).
\(\\[1pt]\)
\({\small 9.\enspace}\) Sam had identical copies of these three paper shapes.
\(\\[1pt]\)

\(\\[1pt]\)
He used them to create these designs.
\(\\[1pt]\)

\(\\[1pt]\)
What value must
x be?
(a). 10
(b). 11
(c). 12
(d). 13
Firstly, we can subtract design 3 area from design 1. The result gives twice of the trapezium area.
So, the area of the trapezium is
\(\\[7pt] \hspace{1.2em} {\small \ = \ (17 \ – \ 5) \ \div \ 2 }\)
\(\\[15pt] \hspace{1.2em} {\small \ = \ 6 \ \mathrm{cm^{2}} }\)
Next, we find the area of the rectangle by subtracting the design 2 area from twice of the trapezium area.
So, the area of the rectangle is
\(\\[7pt] \hspace{1.2em} {\small \ = \ 20 \ – \ 2 \ \times \ 6 }\)
\(\\[15pt] \hspace{1.2em} {\small \ = \ 8 \ \mathrm{cm^{2}} }\)
Lastly, we find the area of the semi-ellipse by subtracting the design 1 area from the trapezium and rectangle area.
So, the area of the semi-ellipse is
\(\\[7pt] \hspace{1.2em} {\small \ = \ 17 \ – \ 6 \ – \ 8 \ }\)
\(\\[15pt] \hspace{1.2em} {\small \ = \ 3 \ \mathrm{cm^{2}} }\)
The area of design 4 is simply the sum of the area of the trapezium and the rectangle minus the semi-ellipse area.
The area of the semi-ellipse (=x) is
\(\\[7pt] \hspace{1.2em} {\small \ = \ 6 \ + \ 8 \ – \ 3 \ }\)
\(\hspace{1.2em} {\small \ = \ 11 \ \mathrm{cm^{2}} \ (b).}\)
\(\\[1pt]\)
\({\small 10.\enspace}\) In the equation below,
A and
B represent natural numbers. What values of
A and
B will make the equation true?
\(\\[1pt]\)
\({\large \frac{A}{3} \ + \ \frac{B}{4} \ = \ \frac{11}{12}} \)
Make the denominator to be the same by finding the LCM between 3 & 4.
\(\\[1pt]\)
\({\large \frac{4A}{12} \ + \ \frac{3B}{12} \ = \ \frac{11}{12}} \)
\(\\[1pt]\)
We find the corresponding equation:
\(\\[1pt]\)
\({\small 4A \ + \ B \ = \ 12}\)
\(\\[1pt]\)
Since, A and B represent natural numbers, the only possible values for A and B are 2 and 1, respectively.
As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .





Calculate logarithm numbers with or without mathematical tables
Use your knowledge about the properties of triangle and make use of congruency notation
Emma wants to plot every point on the number plane where:
– the coordinates are integers
– it is less than 4 units from the origin
– the sum of the coordinates is even or zero
Emma wants to plot every point on the number plane where:
– the coordinates are integers
– it is less than 3 units from the origin
– the sum of the coordinates is even or zero
Tala is sending three parcels. The middle-sized parcel is twice the mass of the smallest parcel and half the mass of the largest parcel. The total mass of the parcels is 840 grams. What is the mass of Tala’s largest parcel?