Logarithmic and Exponential Functions
Logarithmic functions and exponential functions are closely related in such a way that they are inverses of each other.
To be able to solve the questions for this topic, some of the key points that will be needed are:
– the definitions of log and exp functions to convert the form between the two
– the use of laws of logarithms and laws of exponents
– the relationship as the inverses to each other in graphing the two functions
– transforming the exp functions as a straight-line equation in log functions
The definition of logarithmic function:
\( \hspace{3em} {\large y = a^{x} \ \Rightarrow \ \log_{a} y = x } \)
In words:
If \({\small y }\) is base of \({\small a }\) raised to the power of \({\small x }\) then logarithm to the base of \({\small a }\) of \({\small y }\) is \({\small x}\).
For example, if \({\small 8 = 2^3 \ \Rightarrow \ \log_{2} 8 = 3}\)
To solve a more complex problems in logarithmic and exponential functions, we can employ laws of logarithms and laws of exponents as our arsenals.
The laws of logarithms are:
\({\large 1.\hspace{2em} \log_{a} 1 = 0 }\)
\({\large 2.\hspace{2em} \log_{a} a = 1 }\)
\({\large 3.\hspace{2em} \log_{a} {bc} = \log_{a} {b} \ + \ \log_{a} {c} }\)
\({\large 4.\hspace{2em} \log_{a} ({\frac{b}{c}}) = \log_{a} {b} \ – \ \log_{a} {c} }\)
\({\large 5.\hspace{2em} \log_{a^n} {b}^{m} = (\frac{m}{n}) \times \log_{a} b }\)
\({\large 6.\hspace{2em} \log_{a} b = \frac{1}{\log_{b} a} }\)
\({\large 7.\hspace{2em} \log_{a} b = \frac{\log_{p} b}{\log_{p} a} }\)
\({\large 8.\hspace{2em} a^{\log_{a} b} = b}\)
And, the laws of exponents are:
\({\large 1.\hspace{2em} a^{0} = 1; \ a \neq 0 }\)
\({\large 2.\hspace{2em} a^{m} \times a^{n} = a^{m \ + \ n} }\)
\({\large 3.\hspace{2em} \frac{ a^{m} }{ a^{n} } = a^{m \ – \ n} }\)
\({\large 4.\hspace{2em} a^n \ \times \ b^n = {(ab)}^{n} }\)
\({\large 5.\hspace{2em} \frac{ a^{n} }{ b^{n} } = (\frac{a}{b})^{n}}\)
\({\large 6.\hspace{2em} {(a^{m})}^{n} = a^{mn} }\)
\({\large 7.\hspace{2em} \sqrt[n]{a^{m}} = a^{\frac{m}{n}} }\)
\({\large 8.\hspace{2em} \frac{1}{a^n} = a^{-n} }\)
The graph of logarithmic functions are shown as below:
The logarithmic function \({\small y = \log_{a} x}\) has a vertical asymptote at the y-axis and x-intercept at (1, 0).
For base: \({\small 0 < a < 1 }\), the logarithmic function is a monotonic decreasing function.
For base: \({\small a > 1 }\), the logarithmic function is a monotonic increasing function.
Meanwhile, the graph of exponential functions are shown below:
The exponential function \({\small y = a^x}\) has a horizontal asymptote at the x-axis and y-intercept at (0, 1).
For base: \({\small 0 < a < 1 }\), the exponential function is a monotonic decreasing function.
For base: \({\small a > 1 }\), the exponential function is a monotonic increasing function.
If we put both graphs of logarithmic and exponential functions together, it is easy to see that they are reflection of each other to the line y = x.
The exponential functions are widely use in many areas for example in describing the population growth or decay, time value of money with its depreciation or inflation nature and many others.
It is usually helpful to convert the exponential model to a linear model.
Let our exponential growth function be \( N = ka^t\) where \(k\) and \(a\) are constants,
Taking logarithms to both side of the equation gives:
\( \hspace{2em} \log N = \log (ka^t) \)
\( \hspace{2em} \log N = \log a^t + \log k \)
\( \hspace{2em} \log N = \log a . t + \log k \)
Compare that to the straight-line equation: \( y = mx + c\) with:
– the dependent variable \( y = \log N\),
– the gradient \(m = \log a\),
– the independent variable \(x = t\) and
– the y-intercept \( = \log k\)
The y-intercept is the initial population or capital at \(t = 0\).
The gradient represents how fast the population grown.
Try some of the examples below and if you need any help, just look at the solution I have written. Cheers ! =) .
\(\\[1pt]\)
EXAMPLE:
\(\\[1pt]\)
Solve the equation \({\ln (1 + 2^{x}) = 2}\), giving your answer correct to 3 decimal places.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 2.\enspace}\) 9709/32/F/M/19 – Paper 32 March 2019 Pure Maths 3 No 1
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{i}).\hspace{0.8em}}\) Show that the equation \({ \log_{10} (x-4) = 2 \ – \ \log_{10} x} \) can be written as a quadratic equation in \(x\).
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{ii}).\hspace{0.8em}}\) Hence solve the equation \({ \log_{10} (x-4) = 2 \ – \ \log_{10} x }\) giving your answer correct to 3 significant figures.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 3.\enspace}\) 9709/33/M/J/19 – Paper 33 June 2019 Pure Maths 3 No 1
\(\\[1pt]\)
Use logarithms to solve the equation \( 5^{3 \ – \ 2 x} = 4(7^{x})\), giving your answer correct to 3 decimal places.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 4.\enspace}\) 9709/31/M/J/19 – Paper 31 June 2019 Pure Maths 3 No 2
\(\\[1pt]\)
Showing all necessary working, solve the equation
\(\\[1pt]\)
\(\hspace{2em} \ln (2x \ – \ 3) = 2 \ \ln x \ – \ \ln (x \ – \ 1) \)
\(\\[1pt]\)
Give your answer correct to 2 decimal places.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 5.\enspace}\) 9709/32/F/M/20 – Paper 32 March 2020 Pure Maths 3 No 2
\(\\[1pt]\)
Solve the equation \( \ln 3 + \ln (2x+5) = 2 \ \ln(x+2) \).
\(\\[1pt]\)
Give your answer in a simplified exact form.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 6.\enspace}\) 9709/31/M/J/20 – Paper 31 June 2020 Pure Maths 3 No 1
\(\\[1pt]\)
Find the set of values of \( x \) for which \( 2(3^{1-2x}) \lt 5^{x} \).
\(\\[1pt]\)
Give your answer in a simplified exact form.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 7.\enspace}\) 9709/32/M/J/20 – Paper 32 June 2020 Pure Maths 3 No 2
\(\\[1pt]\)
\(\\[1pt]\)
The variables \(x\) and \(y\) satisfy the equation \(y^2 = A {\mathrm{e}}^{kx}\), where \(A\) and \(k\) are constants. The graph of \(\ln y\) against \(x\) is a straight line passing through the points (1.5, 1.2) and (5.24, 2.7) as shown in the diagram.
\(\\[1pt]\)
Find the values of \(A\) and \(k\) correct to 2 decimal places.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 8.\enspace}\) 9709/33/M/J/20 – Paper 33 June 2020 Pure Maths 3 No 3
\(\\[1pt]\)
\({\small (\textrm{a}).\hspace{0.8em}}\) Show that the equation
\(\\[1pt]\)
\(\hspace{2em} \ln (1 + \mathrm{e}^{−x}) + 2x = 0 \)
\(\\[1pt]\)
can be expressed as a quadratic equation in \( \mathrm{e}^{x}\).
\(\\[1pt]\)
\({\small (\textrm{b}).\hspace{0.8em}}\) Hence solve the equation \( \ln (1 + \mathrm{e}^{−x}) + 2x = 0\), giving your answer correct to 3 decimal places.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 9.\enspace}\) 9709/31/O/N/20 – Paper 31 Nov 2020 Pure Maths 3 No 4
\(\\[1pt]\)
Solve the equation
\(\\[1pt]\)
\(\hspace{2em} \log_{10} (2x + 1) = 2 \ \log_{10} (x+1) \ – \ 1 \).
\(\\[1pt]\)
Give your answer correct to 3 decimal places.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 10.\enspace}\) 9709/32/F/M/21 – Paper 32 March 2021 Pure Maths 3 No 1
\(\\[1pt]\)
Solve the equation \( \ln (x^3 − 3) = 3 \ln x − \ln 3 \). Give your answer correct to 3 significant figures.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 11.\enspace}\) 9709/31/M/J/21 – Paper 31 June 2021 Pure Maths 3 No 2
\(\\[1pt]\)
Find the real root of the equation \(\frac{2\mathrm{e}^x \ + \ \mathrm{e}^{-x}}{2 \ + \ \mathrm{e}^x} = 3\), giving your answer correct to 3 decimal places. Your working should show clearly that the equation has only one real root.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 12.\enspace}\) 9709/32/M/J/21 – Paper 32 June 2021 Pure Maths 3 No 3
\(\\[1pt]\)
The variables \(x\) and \(y\) satisfy the equation \(x = A(3^{−y})\), where \(A\) is a constant.
\(\\[1pt]\)
\({\small(\textrm{a}).\hspace{0.8em}}\) Explain why the graph of \(y\) against \( \ln x\) is a straight line and state the exact value of the gradient
of the line.
\(\\[1pt]\)
It is given that the line intersects the \(y\)-axis at the point where \(y\) = 1.3.
\(\\[1pt]\)
\({\small(\textrm{b}).\hspace{0.8em}}\) Calculate the value of \(A\), giving your answer correct to 2 decimal places.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 13.\enspace}\) 9709/33/M/J/21 – Paper 33 June 2021 Pure Maths 3 No 2
\(\\[1pt]\)
Solve the equation \(4^x = 3 + 4^{−x}\). Give your answer correct to 3 decimal places.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 14.\enspace}\) 9709/32/F/M/22 – Paper 32 March 2022 Pure Maths 3 No 3
\(\\[1pt]\)
\(\\[1pt]\)
The variables \(x\) and \(y\) satisfy the equation \( {\small {x}^{n}{y}^{2} \ = \ C } \), where \(n\) and \(C\) are constants.
\(\\[1pt]\)
The graph of \( {\small \ln \ y }\) against \( {\small \ln \ x }\) is a straight line passing through the points (0.31, 1.21) and (1.06, 0.91), as shown in the diagram.
\(\\[1pt]\)
Find the value of \(n\) and find the value of \(C\) correct to 2 decimal places.
\(\\[1pt]\)
\(\\[1pt]\)
PRACTICE MORE WITH THESE QUESTIONS BELOW!
\({\small 1.\enspace}\) Solve the inequality \( |3^x – 5 | \lt 1 \), giving 3 significant figures in your answer.
\({\small 2. \enspace}\) Given that \(x = 4(3^{-y}) \), express \(y\) in terms of \(x\).
\({\small 3. \enspace}\) Using the substitution \(u = 3^{x}\), or otherwise, solve, correct to 3 significant figures, the equation
\(\hspace{2em} 3^{x} = 2 + 3^{-x}\).
\({\small 4. \enspace}\) The variables \(x\) and \(y\) satisfy the relation \(3^y = 4^{x+2}\).
\({\small\hspace{1.2em} (\textrm{a}).\hspace{0.8em}}\) By taking logarithms, show that the graph of \(y\) against \(x\) is a straight line. Find the exact value of the gradient of this line.
\({\small\hspace{1.2em} (\textrm{b}).\hspace{0.8em}}\) Calculate the \(x\) co-ordinate of the point of intersection of this line with the line \(y = 2x\), giving your answer correct to 2 decimal places.
\({\small 5. \enspace}\) It is given that \( \ln(y + 5) – \ln y = 2 \ln x \). Express \(y\) in terms of \(x\), in a form not involving logarithms.
\({\small 6. \enspace}\) Given that \( {(1.25)}^{x} = {(2.5)}^{y}\), use logarithms to find the value of \( \frac{x}{y} \) correct to 3 significant figures.
\({\small 7. \enspace}\) Solve, correct to 3 significant figures, the equation
\( \hspace{2em} \mathrm{e}^x + \mathrm{e}^{2x} = \mathrm{e}^{3x} \).
\({\small 8. \enspace}\) The variables \(x\) and \(y\) satisfy the equation \( y = A(b^{–x}) \), where \(A\) and \(b\) are constants. The graph of \( \ln y \) against \(x\) is a straight line passing through the points (0, 1.3) and (1.6, 0.9), as shown in the diagram. Find the values of \(A\) and \(b\), correct to 2 decimal places.
\(\\[1pt]\)
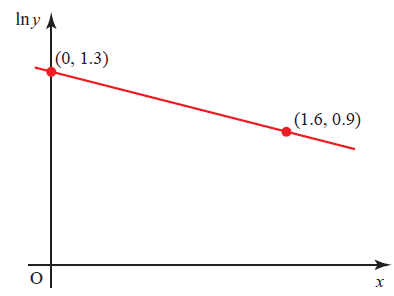
\(\\[1pt]\)
\({\small 9. \enspace}\) Solve the equation \( \ln (2 + \mathrm{e}^{-x}) = 2 \), giving your answer correct to 2 decimal places.
\({\small 10.\enspace}\) Two variable quantities \(x\) and \(y\) are related by the equation \( y = A{x}^{n} \), where \(A\) and \(n\) are constants. The diagram shows the result of plotting \( \ln y \) against \( \ln x \) for four pairs of values of \(x\) and \(y\). Use the diagram to estimate the values of \(A\) and \(n\).
\(\\[1pt]\)
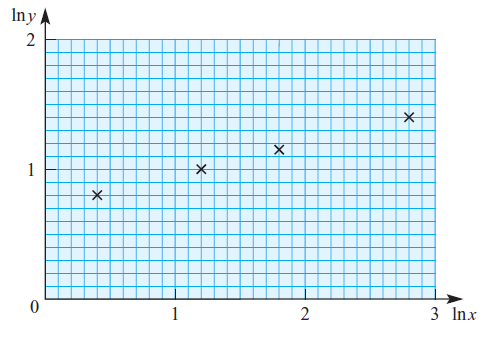
As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .