Try some of the examples below and if you need any help, just look at the solution I have written. Cheers ! =) .
\(\\[1pt]\)
\({\small 1.\enspace}\) In the figure below,
ABC is an isosceles triangle, \({\small \angle {A} = 90^{\large{\circ}}}\) and
PQRS is a square of side 1 cm. Find the area of \({\small \triangle ABC}\).
\(\\[1pt]\)

\(\\[1pt]\)
Since \({\small \triangle ABC}\) is an isosceles right triangle, it has the same side lengths and angles of \({\small 45^{\large{\circ}}}\).
\(\\[1pt]\)
Each of the small triangles inside \({\small \triangle ABC}\) is also an isosceles right triangle \({\small (\triangle BPR, \triangle APQ}\) and \({\small \triangle CQS) }\) are isosceles right triangles.
\(\\[1pt]\)

\(\\[1pt]\)
So, with
BC now known to be 3 cm, the side lengths of
AB and
AC can be found using the
Pythagoras theorem.
\(\\[1pt]\)
\(\\[7pt]\hspace{2.1em} \) Let \({\small AB = AC = x}\)
\(\\[7pt]\hspace{2.1em} {\small {BC}^2 \ = \ {AB}^2 \ + \ {AC}^2 }\)
\(\\[7pt]{\small\hspace{3em}} {\small {3}^2 \ = \ x^2 \ + \ x^2 }\)
\(\\[7pt]{\small\hspace{2.5em}} {\small 2x^2 \ = \ 9 }\)
\(\\[15pt]{\small\hspace{3.2em}} x \ = \ \sqrt{\frac{9}{2}} \)
\(\\[15pt]{\small\hspace{3.2em}} x \ = \ \frac{3}{2}\sqrt{2} \ \mathrm{cm} \)
Finally, we can now find the area of \({\small \triangle ABC}\),
\(\\[1pt]\)
\(\\[10pt] \hspace{4.8em} = \frac{1}{2} \times {\small AB} \times {\small AC} \)
\(\\[10pt] \hspace{4.8em} = \frac{1}{2} \times \frac{3}{2}\sqrt{2} \times \frac{3}{2}\sqrt{2} \)
\(\hspace{4.8em} {\small = \ 2.25 \,\mathrm{{cm}^{2}}} \)
\(\\[1pt]\)
\({\small 2.\enspace}\) In the figure below,
ABEG is a rectangle with
E and
G are the centres of the circles. If
BE \(=\) 7 cm and the areas of the green regions
ABC and
CDF are equal, find
GE.
\(\\[1pt]\)

\(\\[1pt]\)
The area of rectangle
ABEG equals to the area of semi-circle or area of two quadrants. The areas of the green regions cancel each other since they are equal in size. To better understand this, please look at the figure below.
\(\\[1pt]\)

\(\\[1pt]\)
With that knowledge, we can create an equation relating the area of rectangle
ABEG and the area of semi-circle to find
GE.
\(\\[1pt]\)
\(\\[7pt] \hspace{1.2em}\) Area of rectangle \(=\) Area of semi-circle
\(\\[10pt] \hspace{2.1em} {\small AG} \times {\small GE} \ = \frac {1}{2} \times \pi \times r^2 \)
\(\\[10pt] \hspace{2.8em} {\small 7} \times {\small GE} \ = \frac {1}{2} \times \pi \times 7^2 \)
\(\\[10pt] \hspace{4.4em} {\small GE} \ = \frac {\pi \ \times \ {7}^{2}}{2 \ \times \ 7} \)
\(\hspace{4.4em} {\small GE \ = \ 11 \ \mathrm{cm} }\)
\(\\[1pt]\)
\({\small 3.\enspace}\) If rectangle
ABCD is three times as large as \({\small \triangle CDX}\) and four times as large as \({\small \triangle BCY}\), what fraction of the rectangle is coloured orange?
\(\\[1pt]\)

\(\\[1pt]\)
We can tackle this problem by using working out the ratio of areas between the triangles and the rectangle.
\(\\[1pt]\)
\(\\[10pt]\) Area of \({\small \triangle CDX \ = \ } \frac {1}{3} \times \) Area of rectangle ABCD
\(\\[15pt]\hspace{0.7em} \frac{1}{2} {\small \times DC \times DX \ = \ } \frac {1}{3} {\small \times DC \times AD }\)
\(\\[10pt]\) Cancel out DC from both sides of the equation,
\(\\[10pt]{\small\hspace{3em}} {\small {\large\frac{1}{2}} \times DX \ = \ {\large \frac {1}{3}} \times AD}\)
\( \hspace{4.9em} {\small DX \ = \ {\large \frac {2}{3}}AD}\)
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[10pt]\) Area of \({\small \triangle BCY \ = \ } \frac {1}{4} \ \times \) Area of rectangle ABCD
\(\\[15pt]\hspace{0.7em} \frac{1}{2} {\small \times BC \times BY \ = \ } \frac {1}{4} {\small \times BC \times AB }\)
\(\\[10pt]\) Cancel out BC from both sides of the equation,
\(\\[10pt]{\small\hspace{3em}} {\small {\large\frac{1}{2}} \times BY \ = \ {\large \frac {1}{4}} \times AB}\)
\(\hspace{4.9em} {\small BY \ = \ {\large \frac {1}{2}}AB}\)
\(\\[1pt]\)
Finally, we can find the area of \({\small \triangle AXY}\) as a fraction of rectangle ABCD.
\(\\[1pt]\)
\(\\[10pt]\) Area of \({\small \triangle AXY} \ = \ {\small {\large\frac{1}{2}} \times AX \times AY }\)
\(\\[10pt]\hspace{4em} = \ {\small {\large\frac{1}{2}} \times (AD \ – \ DX) \times (AB \ – \ BY)}\)
\(\\[10pt]\hspace{4em} = \ {\small {\large\frac{1}{2}} \times (AD \ – \ {\large \frac {2}{3}}AD) \times (AB \ – \ {\large \frac {1}{2}}AB) }\)
\(\\[10pt]\hspace{4em} = \ {\small {\large\frac{1}{2}} \times ({\large \frac {1}{3}}AD) \times ({\large \frac {1}{2}}AB)}\)
\(\\[10pt]\hspace{4em} = \ {\small {\large\frac{1}{12}} \ \times AD \ \times \ AB}\)
\(\hspace{4em} = \ {\small {\large\frac{1}{12}}}\) of area of rectangle ABCD.
\(\\[1pt]\)
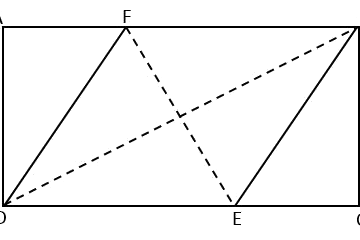
\({\small 4.\enspace}\) In the figure below,
ABCD is a parallelogram.
M and
N are the midpoints of
AD and
BC respectively.
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) What fraction of the parallelogram is the pink area?
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) If the pink area is a rectangle, find the ratio of
AB :
BC.
\(\\[1pt]\)

\(\\[1pt]\)
\({\small\hspace{1.2em}\left(a\right).\enspace}\) If we draw a line connecting
M and
N, we will get two congruent parallelograms,
ABNM and
MNCD.
\(\\[1pt]\)
Each of the parallelograms consists of four triangles which has the same area. Note that the triangles that are opposite to each other are congruent but may not be congruent to the adjacent side triangles. Nevertheless, all four of the triangles still have the same area.
\(\\[1pt]\)

\(\\[1pt]\)
Thus, in parallelogram
ABCD there are 8 triangles with the same area. The pink region consists of two triangles. The fraction of the pink area is then \(\frac{2}{8} \ = \ \frac{1}{4}\)
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(b\right).\enspace}\) If the pink area is a rectangle,
ABNM and
MNCD become two congruent rhombi.
\(\\[1pt]\)
\(\\[10pt] {\small\hspace{1.2em} AB \ = \ BN \ = \ BC }\)
Thus, \({\small AB \ : \ BC \ = \ 1 \ : \ 2 }\)
\(\\[1pt]\)
\({\small 5.\enspace}\)
ABCD is a rhombus.
E and
F are the midpoints of
AD and
CD respectively. What fraction of the rhombus is coloured yellow?
\(\\[1pt]\)

\(\\[1pt]\)
The idea is to use
simple algebra and the formula for areas to find the area of the yellow triangle, \({\small \triangle BEF}\) relative to the area of the rhombus
ABCD.
\(\\[1pt]\)
\(\\[7pt]\hspace{2.1em} \) Let \({\small AE = ED = DF = FC = x}\)
\(\\[7pt]\hspace{2.1em} \) and the height of the rhombus \({ \small \ = \ h }\)
\(\\[1pt]\)
Areas of the small triangles \({\small \triangle ABE, \triangle BCF, \triangle EDF}\) can be expressed in terms of
x and
h.
\(\\[1pt]\)
We can then subtract area of the rhombus
ABCD from areas of the three triangles to get the area of \({\small \triangle BEF}\) relative to area of the rhombus
ABCD.
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[10pt]\) Area of \({\small \triangle ABE} \ = \ {\small {\large\frac{1}{2}} \times x \times h }\)
\(\\[10pt]\hspace{5em} = \ {\small {\large\frac{1}{2}}hx}\)
\(\\[1pt]\)
\(\\[10pt]\) Area of \({\small \triangle BCF} \ = \ {\small {\large\frac{1}{2}} \times 2x \times {\large\frac{1}{2}}h }\)
\(\\[10pt]\hspace{5em} = \ {\small {\large\frac{1}{2}}hx}\)
\(\\[1pt]\)
\(\\[10pt]\) Area of \({\small \triangle EDF} \ = \ {\small {\large\frac{1}{2}} \times x \times {\large\frac{1}{2}}h }\)
\(\\[10pt]\hspace{5em} = \ {\small {\large\frac{1}{4}}hx}\)
\(\\[1pt]\)
\(\\[10pt]\) Area of rhombus
ABCD \( \ = \ {\small 2x \times h }\)
\(\\[10pt]\hspace{5em} = \ {\small 2hx}\)
\(\\[1pt]\)
\(\\[10pt]\) Area of \({\small \triangle BEF} \ = \ {\small 2hx \ – \ {\large\frac{1}{2}}hx \ – \ {\large\frac{1}{2}}hx \ – \ {\large\frac{1}{4}}hx }\)
\(\\[15pt]\hspace{5em} = \ {\small {\large\frac{3}{4}}hx}\)
Thus, the resulting fraction area,
\(\\[17pt]\hspace{3.5em} = \ {\small {\large\frac{{\large\frac{3}{4}}hx}{2hx}}}\)
\(\\[10pt]\hspace{3.5em} = \ {\small {\large\frac{3}{8}}}\)
\(\\[1pt]\)
\({\small 6.\enspace}\)
OAB is a quadrant of radius 7 cm.
OCA and
OCB are semicircles. Find the total area of the red region.
\(\\[1pt]\)

\(\\[1pt]\)
We’ll need to approach this question by observing closely the corresponding shapes inside the quadrant
OAB.
\(\\[1pt]\)
Firstly, we can draw a smaller square that is bounding the petal shape along
OC.
\(\\[1pt]\)

\(\\[1pt]\)
We can then calculate the area of the petal by subtracting the quadrant area from the triangle’s.
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[5pt]\) Area of the petal,
\(\\[10pt] \hspace{2.1em} \ = \ 2 \ \Big[ {\small \frac{1}{4} \times \pi \times {3.5}^{2} \ – \ \frac{1}{2} \times 3.5 \times 3.5 } \Big] \)
\(\\[10pt] \hspace{2.1em} \ = \ 2 \ \Big[ {\small 9.625 \ – \ 6.125} \Big] \)
\(\hspace{2.1em} \ = \ {\small 7 \,\mathrm{{cm}^{2}}} \)
\(\\[1pt]\)
Next, we can find area of the unshaded or white region inside the quadrant
OAB.
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[5pt]\) Area of the unshaded region,
\(\\[10pt] \hspace{2.1em} \ = \ 2 \ \Big[ {\small \frac{1}{2} \times \pi \times {3.5}^{2} \ – \ 7 } \Big] \)
\(\\[10pt] \hspace{2.1em} \ = \ 2 \ \Big[ {\small 19.25 \ – \ 7} \Big] \)
\(\hspace{2.1em} \ = \ {\small 24.5 \,\mathrm{{cm}^{2}}} \)
\(\\[1pt]\)
Finally, we are able to find the total area of the red region by subtracting the quadrant
OAB area from area of the unshaded or white region.
\(\\[1pt]\)
\(\\[5pt]\) Area of the red region,
\(\\[10pt] \hspace{2.1em} \ = \ {\small \frac{1}{4} \times \pi \times {7}^{2} \ – \ 24.5 } \)
\(\\[10pt] \hspace{2.1em} \ = \ {\small 38.5 \ – \ 24.5} \)
\(\hspace{2.1em} \ = \ {\small 14 \,\mathrm{{cm}^{2}}} \)
\(\\[1pt]\)
\({\small 7.\enspace}\) Given that
AB :
BC \(=\)
EF :
FG \(=\) 1 : 2,
CD :
DE \(=\) 2 : 3 and
ACEG is a rectangle, find the ratio of the areas of parts
P,
Q,
R and
S.
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[7pt]\hspace{2.1em} \) Let the length of the rectangle,
\(\\[7pt]\hspace{2.1em} {\small AC = GE = l}\)
\(\\[7pt]\hspace{2.1em} \) Let the width of the rectangle,
\(\\[7pt]\hspace{2.1em} {\small AG = CE = w}\)
\(\\[1pt]\)
Areas of
P, Q, R and S can be expressed in terms of \({\small l}\) and \({\small w}\).
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[10pt]\) Area of \({\small \triangle P} \ = \ {\small {\large\frac{1}{2}} \times {\large\frac{1}{3}}l \times w }\)
\(\\[10pt]\hspace{5em} = \ {\small {\large\frac{1}{6}}lw}\)
\(\\[1pt]\)
\(\\[10pt]\) Area of \({\small \triangle Q} \ = \ {\small {\large\frac{1}{2}} \times {\large\frac{2}{3}}l \times w }\)
\(\\[10pt]\hspace{5em} = \ {\small {\large\frac{1}{3}}lw}\)
\(\\[1pt]\)
\(\\[10pt]\) Area of \({\small \triangle S} \ = \ {\small {\large\frac{1}{2}} \times {\large\frac{2}{3}}l \times {\large\frac{2}{5}}w }\)
\(\\[10pt]\hspace{5em} = \ {\small {\large\frac{2}{15}}lw}\)
\(\\[1pt]\)
Area of \({\small R} \ = \ \) Area of rectangle
ACEG – Area of \({\small \triangle P \ + \ \triangle Q \ + \ \triangle S }\)
\(\\[1pt]\)
\(\\[10pt]\hspace{4.3em} = \ {\small lw \ – \ \big[ {\large\frac{1}{6}}lw \ + \ {\large\frac{1}{3}}lw \ + \ {\large\frac{2}{15}}lw \big]}\)
\(\\[10pt]\hspace{4.3em} = \ {\small {\large\frac{11}{30}}lw}\)
\(\\[1pt]\)
Thus, the ratio of the areas of parts
P,
Q,
R and
S,
\(\\[7pt]\hspace{5em} {\small P \quad : \quad Q \quad : \quad R \quad : \quad S \ }\)
\(\\[15pt]\hspace{3.5em} = \ {\small {\large\frac{1}{6}}lw \ : \ {\large\frac{1}{3}}lw \ : \ {\large\frac{11}{30}}lw \ : \ {\large\frac{2}{15}}lw }\)
\(\hspace{3.5em} = \ { \ \small 5 \quad : \quad 10 \quad : \quad 11 \quad : \quad 4 }\)
\(\\[1pt]\)
\({\small 8.\enspace}\) The shape shown below is bounded by the arc of a three-quarter circle of radius 1 cm and the arcs of two quadrants with radii 2 cm and 3 cm. Find the area of the shape.
\(\\[1pt]\)

\(\\[1pt]\)
The same shape is redrawn with the corresponding radii as sides of the
imaginary rectangles and square.
\(\\[1pt]\)

\(\\[1pt]\)
And then, we will calculate two areas, the yellow region and the cyan region.
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[5pt]\) Area of the yellow region,
\(\\[10pt] \hspace{2.1em} \ = {\small 2 \times 2 \ – \ \frac{1}{4} \times \pi \times {2}^{2} } \)
\(\hspace{2.1em} \ = \ ({\small 4 \ – \ \pi) \,\mathrm{{cm}^{2}}} \)
\(\\[1pt]\)
\(\\[5pt]\) Area of the cyan region,
\(\\[10pt] \hspace{2.1em} \ = {\small 2 \times 1 \ – \ \frac{1}{4} \times \pi \times {1}^{2} } \)
\(\hspace{2.1em} \ = \ \Big({\small 2 \ – \ {\large\frac{\pi}{4}}} \Big) \,{\small \mathrm{{cm}^{2}}} \)
\(\\[1pt]\)
Finally, we can find the total area by adding the two areas, please see the image for better view.
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[5pt]\) The left side area,
\(\\[15pt] \hspace{2.1em} \ = {\small \frac{1}{4} \times \pi \times {3}^{2} \ – \ \bigg[ (4 \ – \ \pi) \ + \ \Big({\small 2 \ – \ {\large\frac{\pi}{4}}} \Big) \bigg] } \)
\(\hspace{2.1em} \ = \ \Big({\small {\large\frac{14}{4}}\pi \ – \ 6} \Big) \,{\small \mathrm{{cm}^{2}}} \)
\(\\[1pt]\)
\(\\[5pt]\) The right side area,
\(\\[10pt] \hspace{2.1em} \ = {\small \frac{1}{2} \times \pi \times {1}^{2} } \)
\(\hspace{2.1em} \ = \ \Big({\small {\large\frac{\pi}{2}}} \Big) \,{\small \mathrm{{cm}^{2}}} \)
\(\\[1pt]\)
\(\\[5pt]\) Thus, the total area,
\(\\[15pt] \hspace{2.1em} \ = \Big({\small {\large\frac{14}{4}}\pi \ – \ 6} \Big) \ + \ \Big({\small {\large\frac{\pi}{2}}} \Big) \)
\(\\[15pt] \hspace{2.1em} \ = \ \Big({\small {\large\frac{16}{4}}\pi \ – \ 6} \Big) \)
\(\\[15pt] \hspace{2.1em} \ \approx \ {\small 6.57 \, \mathrm{{cm}^{2}}} \)








Comment is that i am not understand