Congruent and Similar Triangles
Similar Triangles
Similar triangles are two triangles that have the same shape but not identical or not same size.
In 2 similar triangles, the corresponding angles are equal and the corresponding sides have the same ratio.
There are 3 ways of Similarity Tests to prove for similarity between two triangles:
1. AAA (Angle, Angle, Angle)
If two angles are equal (which implies three angles of the two triangles are equal) then the triangles are similar.
2. Equal ratio of 3 corresponding sides
\( \hspace{3em} {\large\frac{a_{1}}{a_{2}}} \ = \ {\large\frac{b_{1}}{b_{2}}} \ = \ {\large\frac{c_{1}}{c_{2}}} \ = \ k \)
3. Equal ratio of 2 corresponding sides and equal angle in between the two sides
\(\\[20pt] \hspace{3em} {\large\frac{a_{1}}{a_{2}}} \ = \ {\large\frac{b_{1}}{b_{2}}} \ = \ k \)
\(\\[20pt] \hspace{2.9em} {\small \angle B_{1} \ = \ \angle B_{2} }\)
Congruent Triangles
Congruent triangles are two triangles that have the same shape and identical or same size.
In 2 congruents triangles, the corresponding angles and the corresponding sides are equal.
There are 4 ways of Congruence Tests to prove for congruence between two triangles:
1. SSS (Side, Side, Side)
Each corresponding sides of congruent triangles are equal (side, side, side).
2. SAS (Side, Angle, Side)
Two corresponding sides and the angle in between of two congruent triangles are equal (side, angle, side).
3. AAS (Angle, Angle, Side)
Two angles and another opposide side of two congruent triangles are equal (angle, angle, side).
4. RHS (Right Angle, Hypotenuse, Side)
The hypotenuse and one perpendicular side of two congruent right-angled triangles are equal (right angle, hypotenuse, side).
Try some of the examples below and if you need any help, just look at the solution I have written. Cheers ! =) .
\(\\[1pt]\)
EXAMPLE:
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 2.\enspace}\) Name the triangle which is similar to triangle PQR and calculate the values of the unknown lengths.
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{a}).\hspace{0.8em}}\)
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{b}).\hspace{0.8em}}\)
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{c}).\hspace{0.8em}}\)
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{d}).\hspace{0.8em}}\)
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 3.\enspace}\) In the diagram, AB = 5 cm, BD = 12 cm and DE = 7 cm. Calculate BC.
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 4.\enspace}\) In the diagram shown, PQ, LM and RS are parallel. If PQ = 6 cm, RS = 10 cm, calculate the length of LM.
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
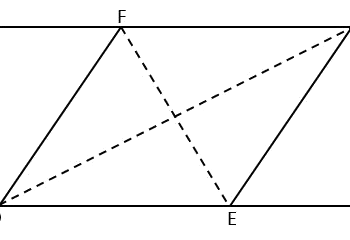
\({\small 5.\enspace}\) Given that \({\small \triangle AED}\) and \({\small \triangle BEC}\) are isosceles triangles, prove that \({\small \triangle ABE}\) and \({\small \triangle EDC}\) are congruent.
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
PRACTICE MORE WITH THESE QUESTIONS BELOW!
\({\small 1.\enspace}\) In the diagram, \({\small AG \parallel BE \ }\) and \({\small CG \parallel DE}\), \({\small AB \ = \ CD \ = \ 10 \ }\) cm and \({\small BC \ = \ 5 \ }\) cm.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{a}).\hspace{0.8em}}\) Name a pair of congruent triangles.
\({\small\hspace{1.2em}(\textrm{b}).\hspace{0.8em}}\) Show that the triangles in (a) are congruent.
\({\small\hspace{1.2em}(\textrm{c}).\hspace{0.8em}}\) Name one triangle that is similar to \({\small \triangle BCF}\).
\({\small\hspace{1.2em}(\textrm{d}).\hspace{0.8em}}\) If \({\small DE \ = \ 6 \ }\) cm, find If \({\small CF }\).
\({\small 2. \enspace}\) In the diagram, ABCD is a quadrilateral. Point X is the intersection of AC and BD. AX = XC and BX = DX.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{a}).\hspace{0.8em}}\) Name a pair of congruent triangles.
\({\small\hspace{1.2em}(\textrm{b}).\hspace{0.8em}}\) Prove that the pair in (a) is congruent.
\({\small\hspace{1.2em}(\textrm{c}).\hspace{0.8em}}\) What is the name given to the quadrilateral ABCD? Explain your answer.
\({\small 3. \enspace}\) Are the triangles below congruent? Explain your answer.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 4. \enspace}\) ABCD is a parallelogram. M is the midpoint of AB and N is the point of intersection betweeen BD and MC.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small\hspace{1.2em} (\textrm{a}).\hspace{0.8em}}\) Name a triangle which is similar to \({\small \triangle MNB }\) and show that they are similar.
\({\small\hspace{1.2em} (\textrm{b}).\hspace{0.8em}}\) Find \({\small {\large \frac{MB}{DC} } }\).
\({\small\hspace{1.2em} (\textrm{c}).\hspace{0.8em}}\) Find area of \({\small \triangle DNC }\) : area of \({\small \triangle BNM }\).
\({\small 5. \enspace}\) In the diagram, PR = QS, QO = PO and \({\small \angle PSQ \ = \ 32^{\large{\circ}}}\).
\(\\[1pt]\)
\(\\[1pt]\)
\({\small\hspace{1.2em} (\textrm{a}).\hspace{0.8em}}\) Show that \({\small \triangle POS }\) and QOR are congruent, stating your reasons clearly.
\({\small\hspace{1.2em} (\textrm{b}).\hspace{0.8em}}\) Name another pair of congruent triangles.
\({\small 6. \enspace}\) In the diagram, AD is parallel to BC. AD = 9 cm, BC = 15 cm, EC = 8 cm and DC = 7 cm.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small\hspace{1.2em} (\textrm{a}).\hspace{0.8em}}\) Prove that \({\small \triangle ADE }\) is similar to \({\small \triangle CBE }\).
\({\small\hspace{1.2em} (\textrm{b}).\hspace{0.8em}}\) Calculate the length of AE.
\({\small\hspace{1.2em} (\textrm{c}).\hspace{0.8em}}\) Calculate the ratio of \({\small {\large \frac{\textrm{Area of} \ \triangle ADE}{\textrm{Area of} \ \triangle ADC} }}\).
\({\small 7. \enspace}\) ABCD is a rectangle. M is the midpoint of AB and N is a point on CD. MC and BN meet at X.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small\hspace{1.2em} (\textrm{a}).\hspace{0.8em}}\) Prove that \({\small \triangle CXN }\) and \({\small \triangle MXB }\) are similar.
\({\small\hspace{1.2em} (\textrm{b}).\hspace{0.8em}}\) Given that the ratio of the area of \({\small \triangle CXN }\) and \({\small \triangle MXB }\) is 9 : 4. Find the following ratios
\({\small\hspace{2.8em}(\textrm{i}).\hspace{0.7em}}\) CN : MB,
\({\small\hspace{2.8em}(\textrm{ii}).\hspace{0.7em}}\) CN : ND,
\({\small\hspace{2.8em}(\textrm{iii}).\hspace{0.5em}}\) area of \({\small \triangle BXC }\) : area of \({\small \triangle BXM }\).
\({\small 8. \enspace}\) In the diagram, ABCD is a rectangle and DEFG is a square. AEB and BCG are straight lines. Show that \({\small \angle ADE \ }\) is equal to \({\small \angle CDG}\) .
\(\\[1pt]\)
\(\\[1pt]\)
As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .
Sine and Cosine Rule with Area of a Triangle
Sine and Cosine Rule with Area of a Triangle
Being equipped with the knowledge of Basic Trigonometry Ratios, we can move one step forward in our quest for studying triangles.
In the case of scalene triangles (triangles with all different lengths), we can use basic trigonometry to find the unknown sides or angles. In principle, each of these scalene triangles can be disassembled into two right-angled triangles.
The resulting derivation from rewriting the unknown height of the triangle in terms of Sine and Cosine functions are the Sine Rule and Cosine Rule.
\(\textrm{Sine Rule (The Law of Sine):}\)
\(\\[1pt]\)
\({\large\frac{{\sin A}}{a} = \frac{{\sin B}}{b} = \frac{{\sin C}}{c}}\)
\(\\[1pt]\)
\(\\[1pt]\)
\(\textrm{Cosine Rule (The Law of Cosine):}\)
\(\\[1pt]\)
\(a^2 = b^2 + c^2 – 2bc\cos A\)
\(\\[1pt]\)
\(b^2 = a^2 + c^2 – 2ac\cos B\)
\(\\[1pt]\)
\(c^2 = a^2 + b^2 – 2ab\cos C\)
\(\\[1pt]\)
As a consequence of the law of sine, we can neatly put a formula for the area of a triangle:
\(\\[1pt]\)
\(\textrm{Area of}\; \triangle ABC = \frac{1}{2}ab\sin C\)
\(\\[1pt]\)
\(\hspace{6.8em} = \frac{1}{2}ac\sin B\)
\(\\[1pt]\)
\(\hspace{6.8em} = \frac{1}{2}bc\sin A\)
\(\\[1pt]\)
As we will soon see in some of the examples below, there are a few things to remember when you are using these formulas:
– Given two sides and an adjacent angle, or two angles and an adjacent side, the triangle can be solved using the Sine Rule.
– Given two sides and an angle in between, or given three sides to find any of the angles, the triangle can be solved using the Cosine Rule.
– Always try to solve the triangle by applying Cosine Rule before Sine Rule due to the ambiguous case with sine rule.
Now let us discuss a little bit deeper about the ambiguous case with sine rule. It arises due to the periodic nature of the sine wave which oscillates between the value of 1 and -1.
To get a clearer picture of what I mean, take a piece of paper and write down the value of \({\small\sin \theta}\) for \({\small \theta =}\) 0 to 180\(^{\circ}\) with an increment of 45\(^{\circ}\).
Sketch the result and you will notice that the sine value of an angle is equal to the sine value of its supplementary angle.
\(\\[1pt]\)
This relationship implies that depending on the ratio of the side length of the triangle, one might have a unique solution or two (an acute triangle, an obtuse triangle or both).
To ensure that you get the correct solution, always check that the equality on the sine rule holds for each pair of the side and the angle.
\(\\[1pt]\)
EXAMPLE:
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) \(\angle\)BAC
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) AB
\({\small\hspace{1.2em}\left(c\right).\hspace{0.8em}}\) area of \(\triangle\)ABC
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 2.\enspace}\) \(\triangle\)PQR is a triangle in which PR \(=\) 4.6 cm, QR \(=\) 8 cm and \(\angle\)PRQ \(=\) 39\(^{\circ}\). Find the value of:
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) PQ
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) \(\angle\)QPR
\({\small\hspace{1.2em}\left(c\right).\hspace{0.8em}}\) area of \(\triangle\)PQR
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 3.\enspace}\) In \(\triangle\)XYZ, x \(=\) 9 cm, y \(=\) 10.5 cm and z \(=\) 10 cm . Find the size of the largest angle in the triangle.
\(\\[1pt]\)
\({\small 4.\enspace}\) In a triangle \(\triangle\)ABC with AC \(=\) 7.1 cm, AB \(=\) 4.6 cm and \(\angle\)ACB \(=\) 33\(^{\circ}\). Find the value of \(\angle\)ABC.
\(\\[1pt]\)
\({\small 5.\enspace}\) ABCD is a trapezium. AD is parallel to BC, AD \(=\) 2.5 cm, AB \(=\) 3 cm, BC \(=\) 5 cm and \(\angle\)B \(=\) 73\(^{\circ}\). Calculate CD.
\(\\[1pt]\)
\(\\[1pt]\)
PRACTICE MORE WITH THESE QUESTIONS BELOW!
\({\small 1.\enspace}\) Find the missing sides (denoted by small-letter variables) and angles (denoted by capital letters) from each of the triangles below, hence find the area of the triangle.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 2.\enspace}\) A ruined tower is fenced off for safety reasons. To find the height of the tower Rashid stands at a point A and measures the angle of elevation as \({\small 18^{\large{\circ}}}\). He then walks 20 metres directly towards the base of the tower to point B where the angle of elevation is \({\small 31^{\large{\circ}}}\). Calculate the height, h, of the tower.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 3.\enspace}\) ABCD is a quadrilateral. \({\small AB = 7 \ \textrm{cm}, \ AD = 6 \ \textrm{cm} \ \textrm{and} \ BC = 9 \ \textrm{cm}}\). Angle ABC \(= \ {\small 75^{\large{\circ}}}\) and angle ADC \(= \ {\small 90^{\large{\circ}}}\). Calculate the perimeter of ABCD.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 4.\enspace}\) The side of a regular pentagon is 24 cm long. Approximate the radius of the circumscribed circle. (Hint: use Sine Rule).
\({\small 5.\enspace}\) TAC is a triangle. Point B is located along the straight line AC. TB \(=\) 18 cm and TC \(=\) 12 cm. \({\small \angle }\) ATB \( = {\small 61^{\large{\circ}}}\) and \({\small \angle }\) BTC \(= {\small 27^{\large{\circ}}}\). Calculate
\({\small\hspace{1.2em}\left(a\right).\enspace \angle }\) TCB
\({\small\hspace{1.2em}\left(b\right).\enspace}\) TA.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 6.\enspace}\) In the figure, AB \(=\) 3 cm, BC \(=\) 6 cm, CA \(=\) 7 cm, AD \(=\) 8 cm and DC \(=\) 4 cm. Calculate the length of BD.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 7.\enspace}\) In the diagram, BCD is a straight line. BC \(=\) 36 cm, CD \(=\) 24 cm and the area of \({\small \triangle {ACD} \ = \ 178 \ \mathrm{{cm}^{2}}}\). Calculate the area of \({\small \triangle {ABC}}\).
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 8.\enspace}\) Given in the figure, AQ \(=\) 15 cm, QB \(=\) 6.7 cm, AP \(=\) 5.5 cm, PC \(=\) 10.4 cm and \({\small \angle }\) BAC \( = {\small 74^{\large{\circ}}}\). Calculate the area of the quadrilateral PQBC and the length of BC.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 9.\enspace}\) The area of \({\small \triangle {ABD} \ = \ 33.6 \ \mathrm{{m}^{2}}}\). Find the length of CD.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 10.\enspace}\) Jane and Peter are considering buying a block of land. The land agent supplies them with the given accurate sketch. Find the area of the property.
\(\\[1pt]\)
As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .
Challenging Questions on Various Secondary Math Topics
Challenging Questions on Various Secondary Math Topics
I have compiled some of the challenging questions I have covered with my students. For those who are interested, you are more than welcomed to give the questions below a try! Cheers =) .
\(\\[1pt]\)
QUESTIONS:
\(\\[1pt]\)
\({\LARGE\frac{108}{17} \ = \ } {\LARGE a} + \huge{\frac{1}{b \ + \ \frac{1}{c \ + \ \frac{1}{d \ + \ 2}}}}\)
\(\\[1pt]\)
with a, b, c and d are positive integers. Find the value of:
\(\\[1pt]\)
\({\LARGE\frac{a^3 \ – \ 3a^2b \ + \ 3ab^2 \ – \ b^3}{c^3 \ – \ 3c^2d \ + \ 3cd^2 \ – \ d^3}} \)
\(\\[1pt]\)
\({\small 2.\enspace}\) One year, 23 September was a Monday. What day of the week was 10 November that year?
\(\hspace{1.2em}\)(a). Sunday
\(\hspace{1.2em}\)(b). Monday
\(\hspace{1.2em}\)(c). Thursday
\(\hspace{1.2em}\)(d). Saturday
\(\\[1pt]\)
\({\small 3.\enspace}\) In a rectangle ABCD, point F and E are located at the side AB and DC in such a way a rhombus BFDE is formed, as shown in the picture.
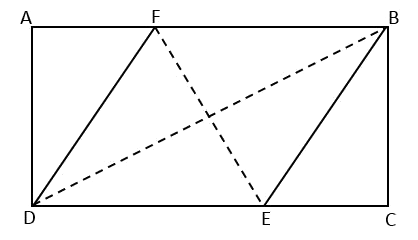
If AB \(=\) 6.4 cm and BC \(=\) 4.8 cm, find EF.
\(\\[1pt]\)
\({\small 4.\enspace}\) Given that: \((3x\:+\:4y \:-\: 5z)^{3}\), find the sum of coefficients of the terms: \(x^2y,\:y^2z\) and \(x^2z\).
\(\\[1pt]\)
\({\small 5.\enspace}\) Find the result of:
\(\\[1pt]\)
\({\large\frac{5}{(2 \ \times \ 3)^{2}}}+{\large\frac{7}{(3 \ \times \ 4)^{2}}}+{\large\frac{9}{(4 \ \times\ 5)^{2}}} + \dots + {\large\frac{23}{(11 \ \times \ 12)^{2}}}\)
\(\\[1pt]\)
\({\small 6.\enspace}\) Mr. Santoso has five kids. Each of them is given a different amount of pocket money per week. Adi gets half of what Edi receives, Beni gets $1 more from Adi, Citra gets $1.5 more than Adi and Doni gets $1.7 less that Edi. If the average of their pocket money is $5.2 in a week, what is the amount of pocket money that Doni received in a year?
\(\\[1pt]\)
\({\small 7.\enspace}\) The same rule is applied to the top number in each box to give the bottom number.
\(\\[1pt]\)
\(\\[1pt]\)
What number must box x be ?
(a). 30
(b). 32
(c). 34
(d). 40
\(\\[1pt]\)
\({\small 8.\enspace}\) Oscar, Lily and Jack collect souvenir coins. Oscar has 44 more coins than Lily and 48 more coins than Jack. Oscar has 6 more coins than Lily and Jack combined. How many coins do Oscar, Lily and Jack have altogether?
(a). 196
(b). 166
(c). 156
(d). 146
\(\\[1pt]\)
\({\small 9.\enspace}\) Sam had identical copies of these three paper shapes.
\(\\[1pt]\)
\(\\[1pt]\)
He used them to create these designs.
\(\\[1pt]\)
\(\\[1pt]\)
What value must x be?
(a). 10
(b). 11
(c). 12
(d). 13
\(\\[1pt]\)
\({\small 10.\enspace}\) In the equation below, A and B represent natural numbers. What values of A and B will make the equation true?
\(\\[1pt]\)
\({\large \frac{A}{3} \ + \ \frac{B}{4} \ = \ \frac{11}{12}} \)
\(\\[1pt]\)
As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .
Bearing and Distance
Bearing and Distance
The bearing and distance is an example of applied knowledge of trigonometry. The navigation used on land, sea or air was done using bearing (at least before GPS was invented and widely used). In this topic, we will learn how to use the bearing to calculate the distance or position of one place to another.
We will use the convention for bearing as follows:
– three-figure or three-digit
– North or N is the reference for \({\small 0^{\large{\circ}}}\)
– measured in the clockwise direction from the North
I have put together some of the questions I received in the comment section below. You can try these questions also to further your understanding on this topic.
To check your answer, you can look through the solutions that I have posted either in Youtube videos or Instagram posts.
You can subscribe, like or follow my youtube channel and IG account. I will keep updating my IG daily post, preferably.
Furthermore, you can find some examples and more practices below! =).
\(\\[1pt]\)
QUESTIONS FROM STUDENTS:
\(\\[1pt]\)
\({\small 2.\enspace}\) A boat sails round a quadrangular course ABCD, starting from A to B in 4 km due east of A, C is 3 km due south of B and D is 4 km S50W from C.
\(\\[1pt]\)
What is the distance and bearing of A from D?
\(\\[1pt]\)
\({\small 3.\enspace}\) \({\small\hspace{0.2em}\left(\textrm{a}\right).\hspace{0.8em}}\) A village is 10 km on a bearing \({\small 050^{\large{\circ}}}\) from a point O. How far is the village North of O?
\(\\[1pt]\)
\({\small\hspace{1.6em}\left(\textrm{b}\right).\hspace{0.8em}}\) The angle of elevation of the top of a building from a point 80 m away on a level ground is \({\small 25^{\large{\circ}}}\).
\(\\[1pt]\)
Calculate the height of the building to the nearest metre.
\(\\[1pt]\)
\({\small 4.\enspace}\) Town F is 50 km east of Town G. Town H is on a bearing of \({\small 040^{\large{\circ}}}\) from Town F. The distance from F to H is 65 km.
\(\\[1pt]\)
Calculate, to the nearest km, the actual distance GH.
\(\\[1pt]\)
Calculate, to the nearest degree, the bearing of H from G.
\(\\[1pt]\)
\({\small 5.\enspace}\) A village R is 10 km from a point P on a bearing \({\small 025^{\large{\circ}}}\) from P. Another village A is 6 km from P on a bearing of \({\small 016^{\large{\circ}}}\). Calculate,
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(\textrm{a}\right).\hspace{0.8em}}\) the distance of R from A and
\({\small\hspace{1.2em}\left(\textrm{b}\right).\hspace{0.8em}}\) the bearing of R from A
\(\\[1pt]\)
\({\small 6.\enspace}\) The bearing of city R from city M is \({\small 058^{\large{\circ}}}\) and the bearing of city K from city M is \({\small 310^{\large{\circ}}}\).
\(\\[1pt]\)
If the distance from M to R is 40 km and that of M to K is 70 km,
\(\\[1pt]\)
What is the distance between K and R to 1 decimal place and bearing of K from R
to the nearest degree?
\(\\[1pt]\)
\({\small 7.\enspace}\) The bearing of two points Q and R from a point P are \({\small 050^{\large{\circ}}}\) and \({\small 120^{\large{\circ}}}\) respectively.
\(\\[1pt]\)
If PQ = 12 cm and PR = 5 cm, find the distance QR.
\(\\[1pt]\)
\({\small 8.\enspace}\) A ship leaves a port at noon and has a bearing of \({\small 207^{\large{\circ}}}\). If the ship is traveling at 20 miles per hour, how many miles south and how many miles west is the ship from its departure point at 6 pm?
\(\\[1pt]\)
\({\small 9.\enspace}\) From a point H at a harbour, the bearing of two ships A and B on the high sea are \({\small 160^{\large{\circ}}}\) and \({\small 220^{\large{\circ}}}\) respectively. B is 14 km from H and the bearing of A from B is \({\small 085^{\large{\circ}}}\).
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(\textrm{a}\right).\hspace{0.8em}}\) How far apart are the two ships?
\({\small\hspace{1.2em}\left(\textrm{b}\right).\hspace{0.8em}}\) What is the bearing of B from A?
\(\\[1pt]\)
\({\small 10.\enspace}\) An aircraft travels 120 km on a bearing of \({\small 062^{\large{\circ}}}\) and then 95 km on a bearing of \({\small 305^{\large{\circ}}}\). How far is the aircraft from the starting point?
\(\\[1pt]\)
\({\small 11.\enspace}\) Two boats A and B left a port C at the same time on different routes. B travelled on a bearing of \({\small 150^{\large{\circ}}}\) and A travelled on north side of B. When A had travelled 8 km and B travelled 10 km, the distance between the two boats was found to be 12 km. Calculate the bearing of A’s route from C.
\(\\[1pt]\)
\({\small 12.\enspace}\) An aeroplane flies from town X on a bearing of \({\small 45^{\large{\circ}}}\)E to another town Y with a distance of 200 km. It then changes course and flies to another town Z on a bearing of S\({\small 60^{\large{\circ}}}\)E. If Z is directly east of X, calculate correct to 3 s.f.:
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(\textrm{a}\right).\hspace{0.8em}}\) the distance from X to Z.
\({\small\hspace{1.2em}\left(\textrm{b}\right).\hspace{0.8em}}\) the distance from Y to XZ.
\(\\[1pt]\)
\({\small 13.\enspace}\) A,B,C are three locations on the same horizontal plane. B is on a bearing of \({\small 041^{\large{\circ}}}\) from A and the distance is 40 km. C is directly due north of A and the distance between B and C is 35 km. Find the bearing of C from B.
\(\\[1pt]\)
\({\small 14.\enspace}\) The bearing of A from B is \({\small 129^{\large{\circ}}}\) and the bearing of C from B is \({\small 219^{\large{\circ}}}\). If B is equidistant from A and C, find the bearing of C from A.
\(\\[1pt]\)
\({\small 14.\enspace}\) A,B,C are three locations on the same horizontal plane. B is on a bearing of \({\small 041^{\large{\circ}}}\) from A and the distance is 40 km. C is directly due north of A and the distance between B and C is 35 km. Find the bearing of C from B.
\(\\[1pt]\)
\({\small 15.\enspace}\) A ship sails 50 km north from a point A, then 25 km west and finally 50 km on a bearing of \({\small 315^{\large{\circ}}}\).
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(\textrm{a}\right).\hspace{0.8em}}\) How far west is the ship from the point A?
\({\small\hspace{1.2em}\left(\textrm{b}\right).\hspace{0.8em}}\) How far north is the ship from the point A?
\({\small\hspace{1.2em}\left(\textrm{c}\right).\hspace{0.8em}}\) Find the distance and bearing of the ship destination from A?
\(\\[1pt]\)
EXAMPLE:
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) Show that \({\small \angle {ACB} = 48^{\large{\circ}}}\).
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) Calculate
\({\small\hspace{2.8em}\left(i\right).\hspace{0.7em}}\) the distance AB,
\({\small\hspace{2.8em}\left(ii\right).\hspace{0.7em}}\) the bearing of A from B,
\({\small\hspace{2.8em}\left(iii\right).\hspace{0.5em}}\) the area of triangle ABC,
\({\small\hspace{2.8em}\left(iv\right).\hspace{0.7em}}\) the shortest distance from B to AC.
\({\small\hspace{1.2em}\left(c\right).\hspace{0.8em}}\) A helicopter, H, is hovering directly above a point D, nearest to B on AC. If the angle of elevation of H seen from B is \({\small 10^{\large{\circ}}}\), calculate the height of H above D.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 2.\enspace}\) A ship leaves port at noon and has a bearing of \({\small 207^{\large{\circ}}}\). If the ship is traveling at 20 miles per hour, how many miles south and how many miles west is the ship from its departure point at 6 pm?
\(\\[1pt]\)
\({\small 3.\enspace}\) From the lookout tower A, a column of smoke is sighted due south. From a second lookout tower B, 5 miles west of A, the smoke is observed with a bearing of \({\small 117^{\large{\circ}}}\). How far is the fire from tower B? How far is it from tower A?
\(\\[1pt]\)
\({\small 4.\enspace}\) Pittsburgh is 117 miles due south of Kansas City. A plane leaves Kansas City at noon and flies 200 mph with a bearing of \({\small 201^{\large{\circ}}}\). When, to the nearest minute, will the plane be due west of Pittsburgh?
\(\\[1pt]\)
\({\small 5.\enspace}\) Two ships A and B leave port at the same time with ship A sailing with a bearing of \({\small 023^{\large{\circ}}}\) at the speed of 11 mph and ship B sailing with a bearing of \({\small 113^{\large{\circ}}}\) at 15 mph. Approximate the bearing from ship B to ship A one hour later.
\(\\[1pt]\)
PRACTICE MORE WITH THESE QUESTIONS BELOW!
\({\small 1.\enspace}\) Two ships, A and B leave port at 13 00 hours. Ship A travels at a constant speed of 18 km per hour on a bearing of \({\small 070^{\large{\circ}}}\). Ship B travels at a constant speed of 25 km per hour on a bearing of \({\small 152^{\large{\circ}}}\). Calculate the distance between A and B at 15 00 hours.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 2. \enspace}\) A plane is 120 miles north and 85 miles east of an airport. If the pilot wants to fly directly to the airport, what bearing should be taken?
\({\small 3. \enspace}\) Ohio is 190 miles due north of Virginia. Stamford is due east of Ohio and is 460 miles from Virginia. What is the bearing angle heading from Virginia to Stamford? What is the bearing angle from Stamford to Virginia?
\({\small 4. \enspace}\) D is 30 km due east of A. A ship sails from A on a certain bearing for 15 km to B. It then sails to C, which is 40 km from A and due north of D. Finally it sails due south to D. AB is the bisector of \({\small \angle {EAC}}\). Calculate the total distance for the whole journey.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 5. \enspace}\) An observer at a radar station plots an aircraft due north of him and at a range of 50 km, measured horizontally. The aircraft keeps on traveling due west at a constant height. The bearing of the plane from the observer 10 minutes later is \({\small 300^{\large{\circ}}}\). Calculate the speed of the aircraft in km/h.
\({\small 6. \enspace}\) N is north of S. NS is the tangent to the circle, radius 1 km, at T. A man walks 2 km along the circle from T to P. What is the distance and bearing of P from T?
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 7. \enspace}\) In the diagram, A, B, C and D are four points on a horizontal field. A is north of B. The bearing of D from A is \({\small 115^{\large{\circ}}}\) and the bearing of D from B is \({\small 25^{\large{\circ}}}\). \({\small \angle {BDC} = 130^{\large{\circ}}}\), BD \(=\) 150 m and CD \(=\) 110 m.
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) Find the value of \({\small \angle {ADB}}\).
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) Find the bearing of B from D.
\({\small\hspace{1.2em}\left(c\right).\hspace{0.8em}}\) Find the bearing of C from D.
\({\small\hspace{1.2em}\left(d\right).\hspace{0.8em}}\) Calculate the shortest distance of point A to line DB.
\({\small\hspace{1.2em}\left(e\right).\hspace{0.8em}}\) Calculate the length of BC.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 8. \enspace}\) In the diagram (not drawn to scale), E, G and C represents three points at the Esplanade, Gardens by the Bay and the City Hall respectively. Given that EG \(=\) 1125 m and CE \(=\) 957 m, the bearing of G from E is \({\small 135^{\large{\circ}}}\) and \({\small \angle {CEG} = 60^{\large{\circ}}}\). Find
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) the bearing of E from C,
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) the distance between C and G,
\({\small\hspace{1.2em}\left(c\right).\hspace{0.8em}}\) \({\small \angle {EGC}}\),
\({\small\hspace{1.2em}\left(d\right).\hspace{0.8em}}\) the bearing of C from G.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 9. \enspace}\) In the diagram, Q is due east of P. Given that PQ \(=\) 55 m and RQ \(=\) 32 m and \({\small \angle {PRQ} = 105^{\large{\circ}}}\). Find
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) The bearing of R from P,
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) The area of \({\small \triangle {PRQ}}\).
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 10.\enspace}\) In the diagram, A, B, C and D are four corners of a field. AD \(=\) 53 m, DC \(=\) 87 m, BC \(=\) 66 m, \({\small \angle {ABC} = 90^{\large{\circ}}}\) and \({\small \angle {ACB} = 58^{\large{\circ}}}\).
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) Calculate AC.
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) The bearing of B from C is \({\small 340^{\large{\circ}}}\). Calculate
\({\small\hspace{2.8em}\left(i\right).\hspace{0.7em}}\) the bearing of A from C,
\({\small\hspace{2.8em}\left(ii\right).\hspace{0.7em}}\) the bearing of A from B.
\({\small\hspace{1.2em}\left(c\right).\hspace{0.8em}}\) Calculate
\({\small\hspace{2.8em}\left(i\right).\hspace{0.7em}}\) the angle of \({\small \angle {ADC}}\),
\({\small\hspace{2.8em}\left(ii\right).\hspace{0.7em}}\) the area of \({\small \triangle {ADC}}\),
\({\small\hspace{2.8em}\left(iii\right).\hspace{0.5em}}\) the shortest distance from A to DC.
\({\small\hspace{1.2em}\left(d\right).\hspace{0.8em}}\) An eagle is hovering vertically above A. The angle of elevation of the eagle from D is \({\small 42^{\large{\circ}}}\). Calculate the greatest angle of elevation of the eagle from a point on DC.
\(\\[1pt]\)
As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .
Basic Trigonometry
Basic Trigonometry
Trigonometry is another big topic in Mathematics. It is the study of measuring triangles, the most basic two-dimensional figure. It has practical application in many areas such as architecture, geometry, physics and others since more complex shapes are just collections of triangles as the building blocks.
To become proficient in trigonometry, a strong knowledge of the Pythagorean Theorem and the right-angled triangle are pivotal. To begin with, the three basic trigonometric functions are described as follows:
\(\\[10pt]\quad{\small 1.\quad}\)\( \sin \theta = \large{\frac{opp}{hyp}}\)
Sine of an angle \(({\small\sin \theta})\) is the ratio of the opposite side (opp) to the hypotenuse (hyp) of a right-angled triangle.
\(\\[10pt]\quad{\small 2.\quad}\)\( \cos \theta = \large{\frac{adj}{hyp}}\)
Cosine of an angle \(({\small\cos \theta})\) is the ratio of the adjacent side (adj) to the hypotenuse (hyp) of a right-angled triangle.
\(\\[10pt]\quad{\small 3.\quad}\)\( \tan \theta = \large{\frac{opp}{adj}}\)
Tangent of an angle \(({\small\tan \theta})\) is the ratio of the opposite side (opp) to the adjacent (adj) of a right-angled triangle.
Generally, small letters (a, b, c, …) are used to represent sides of a triangle and capital letters (A, B, C, …) are used to represent the angle on the opposite side of a triangle side. Please take a look at the illustration below for a clearer usage and notations.
\(\\[1pt]\)
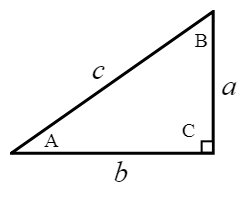
\(\\[1pt]\)
\(\\[15pt]\quad \sin A = \large{\frac{opp}{hyp}=\frac{a}{c}},\)\(\quad \sin B = \large{\frac{opp}{hyp}=\frac{b}{c}}\)
\(\\[15pt]\quad \cos A = \large{\frac{adj}{hyp}=\frac{b}{c}},\)\(\quad \cos B = \large{\frac{adj}{hyp}=\frac{a}{c}}\)
\(\\[15pt]\quad \tan A = \large{\frac{opp}{adj}=\frac{a}{b}},\)\(\quad \tan B = \large{\frac{opp}{adj}=\frac{b}{a}}\)
\(\\[5pt]\)
Use the acronym “SOH”, “CAH”, “TOA” to help you remember these formulas.
Try the exercises below and if you need any help, just look at the solution I have written. Cheers ! =) .
\(\\[1pt]\)
EXAMPLE:
\({\small\hspace{1.2em}\left(i\right).\hspace{0.8em}}\) \({\small\sin X},\quad{\small\hspace{1.2em}\left(iv\right).\hspace{0.5em}}\) \({\small\sin Y}\),
\({\small\hspace{1.2em}\left(ii\right).\hspace{0.5em}}\) \({\small\cos X},\quad{\small\hspace{1.2em}\left(v\right).\hspace{0.7em}}\) \({\small\cos Y}\),
\({\small\hspace{1.2em}\left(iii\right).\hspace{0.2em}}\) \({\small\tan X},\quad{\small\hspace{1em}\left(vi\right).\hspace{0.5em}}\) \({\small\tan Y}\).
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 2.\enspace}\) Find the value of the unknowns in each of the following right-angled triangles.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 3.\enspace}\) A point P on level ground is 43 m away from the top of a vertical post QR of height 32 m. Find \(\angle\)QPR.
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 4.\enspace}\) To travel from school to his home, Ethan can walk along the straight path SH. However, he sometimes take a detour by travelling from school to the food centre F, then from the food centre to his home. Find
\({\small\hspace{1.2em}\left(a\right).\enspace}\)SF, the distance between the school and the food centre,
\({\small\hspace{1.2em}\left(b\right).\enspace}\)FH, the distance between the food centre and his home.
\(\\[1pt]\)
\({\small 5.\enspace}\) In a computer game, a soldier stands on the top of an observatory AB 45 m above the ground. He observes the enemy at the point E. Given that \(\angle\)AEB \({\small= 38^{\circ}}\), find the distance between the enemy and the foot of the observatory.
\(\\[1pt]\)
PRACTICE AND TRY THESE QUESTIONS BELOW!
\({\small 1.\enspace}\) Triangle ABC is a right-angled triangle. Find
\({\small\hspace{1.2em}\left(a\right).\enspace \cos A}\)
\({\small\hspace{1.2em}\left(b\right).\enspace \tan A}\)
\({\small\hspace{1.2em}\left(c\right).\enspace \sin C}\)

\({\small 2.\enspace}\) A man at the top of a vertical cliff observes a boat at the sea. State the angle of depression of the boat from the man.
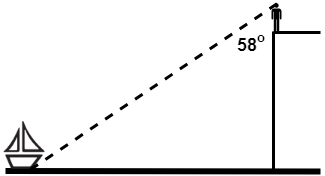
\(\\[1pt]\)
\({\small 3.\enspace}\) The angle of elevation of the top of a building from a point on the ground 220 m away from the foot of the building is 16\(^{\circ}\). What is the height of the building?
\({\small 4.\enspace}\) A boy standing in the middle of two flagpoles 78 m apart finds that the angle of elevation of the tops of the flagpoles from the point where he is standing are 34\(^{\circ}\) and 43\(^{\circ}\). Find the difference in the heights of the two flagpoles.
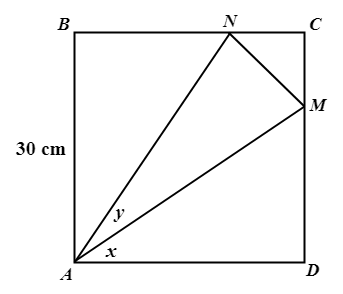
\({\small 5.\enspace}\) In the diagram, ABCD is a square of side 30 cm, CM : MD \(=\) 1 : 2 and \(\angle\)MDA \(=\) \(\angle\)MCN.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Find the exact value of \({\small\tan X}\).
\({\small\hspace{1.2em}\left(b\right).\enspace}\) Find the length of CN.
\({\small\hspace{1.2em}\left(c\right).\enspace}\) Calculate the value of y.
\(\\[1pt]\)
\({\small 6.\enspace}\) If x is an acute angle and \({\small\sin x} = \large{\frac{15}{17}}\), find the exact value of \({\small\cos x}\) and \({\small\tan x}\).
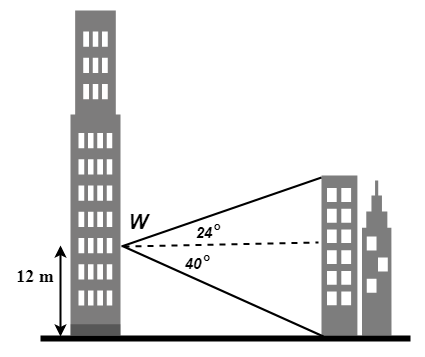
\({\small 7.\enspace}\) From the window, W of a building which is 12 m above the ground level, a man observes that the angle of elevation of the top, A of another building is 24\(^{\circ}\) and the angle of depression of its foot, B is 40\(^{\circ}\). Find the height of the second building.
\(\\[1pt]\)
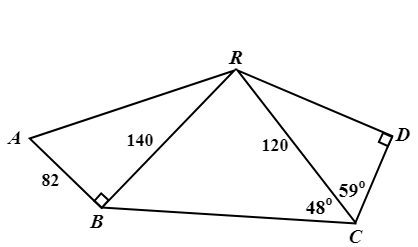
\({\small 8.\enspace}\) The diagram shows footpaths BR and CR in a park ABCDR. BR \(=\) 140 m, CR \(=\) 120 m and AB \(=\) 82 m. \(\angle\)BCR \(=\) 48\(^{\circ}\), \(\angle\)DCR \(=\) 59\(^{\circ}\) and \(\angle\)ABR \(=\) \(\angle\)CDR \(=\) 90\(^{\circ}\). Calculate
\({\small\hspace{1.2em}\left(a\right).\enspace}\) CD,
\({\small\hspace{1.2em}\left(b\right).\enspace}\) \(\angle\)ARB.
\(\\[1pt]\)
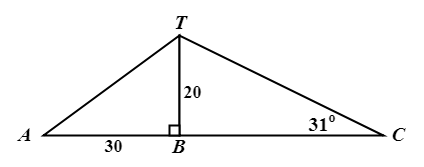
\({\small 9.\enspace}\) A, B and C are three points on horizontal ground. BT is a vertical mast of height 20 m. The top of the mast is joined to A and C by straight wires. \(\angle\)BCT \(=\) 31\(^{\circ}\).
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Calculate the length of the wire CT.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) Given that AB is 30 m, calculate the angle of elevation of T from A.
\(\\[1pt]\)
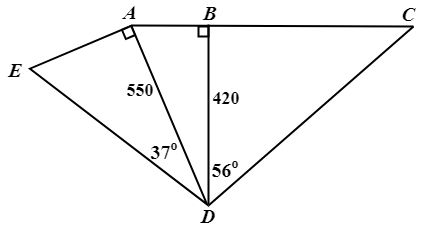
\({\small 10.\enspace}\) The diagram shows the available paths in a park. ABC is a straight line. \(\angle\)EAD \(=\) \(\angle\)ABD \(=\) 90\(^{\circ}\), \(\angle\)ADE \(=\) 37\(^{\circ}\) and \(\angle\)BDC \(=\) 56\(^{\circ}\). BD \(=\) 420 m and AD \(=\) 550 m. Calculate
\({\small\hspace{1.2em}\left(a\right).\enspace}\) AB,
\({\small\hspace{1.2em}\left(b\right).\enspace}\) BC,
\({\small\hspace{1.2em}\left(c\right).\enspace}\) DE.
\(\\[1pt]\)
As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .
Area and Perimeter
Area and Perimeter
Try some of the examples below and if you need any help, just look at the solution I have written. Cheers ! =) .
\(\\[1pt]\)
EXAMPLE:
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 2.\enspace}\) In the figure below, ABEG is a rectangle with E and G are the centres of the circles. If BE \(=\) 7 cm and the areas of the green regions ABC and CDF are equal, find GE.
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 3.\enspace}\) If rectangle ABCD is three times as large as \({\small \triangle CDX}\) and four times as large as \({\small \triangle BCY}\), what fraction of the rectangle is coloured orange?
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 4.\enspace}\) In the figure below, ABCD is a parallelogram. M and N are the midpoints of AD and BC respectively.
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) What fraction of the parallelogram is the pink area?
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) If the pink area is a rectangle, find the ratio of AB : BC.
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 5.\enspace}\) ABCD is a rhombus. E and F are the midpoints of AD and CD respectively. What fraction of the rhombus is coloured yellow?
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 6.\enspace}\) OAB is a quadrant of radius 7 cm. OCA and OCB are semicircles. Find the total area of the red region.
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 7.\enspace}\) Given that AB : BC \(=\) EF : FG \(=\) 1 : 2, CD : DE \(=\) 2 : 3 and ACEG is a rectangle, find the ratio of the areas of parts P, Q, R and S.
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)
\({\small 8.\enspace}\) The shape shown below is bounded by the arc of a three-quarter circle of radius 1 cm and the arcs of two quadrants with radii 2 cm and 3 cm. Find the area of the shape.
\(\\[1pt]\)
\(\\[1pt]\)
\(\\[1pt]\)