Similar triangles are two triangles that have the same shape but not identical or not same size.
If two angles are equal (which implies three angles of the two triangles are equal) then the triangles are similar.
\( \hspace{3em} {\large\frac{a_{1}}{a_{2}}} \ = \ {\large\frac{b_{1}}{b_{2}}} \ = \ {\large\frac{c_{1}}{c_{2}}} \ = \ k \)
\(\\[20pt] \hspace{3em} {\large\frac{a_{1}}{a_{2}}} \ = \ {\large\frac{b_{1}}{b_{2}}} \ = \ k \)
\(\\[20pt] \hspace{2.9em} {\small \angle B_{1} \ = \ \angle B_{2} }\)
Congruent triangles are two triangles that have the same shape and identical or same size.
Each corresponding sides of congruent triangles are equal (side, side, side).
Two corresponding sides and the angle in between of two congruent triangles are equal (side, angle, side).
Two angles and another opposide side of two congruent triangles are equal (angle, angle, side).
The hypotenuse and one perpendicular side of two congruent right-angled triangles are equal (right angle, hypotenuse, side).
Try some of the examples below and if you need any help, just look at the solution I have written. Cheers ! =) .
\(\\[1pt]\)
\({\small 1.\enspace}\) In the diagram, \({\small P\hat{Q}R}\) = \({\small Q\hat{R}S}\) = \({\small R\hat{S}T}\) = \({\small 90^{\large{\circ}}}\), \({\small PQ}\) = \({\small QR}\) = \({\small RS}\) = 5 cm and \({\small ST}\) = 1cm. Find the length of \({\small QU}\).
\(\\[1pt]\)

\(\\[1pt]\)
We can extend \({\small PQ}\) and \({\small TS}\) to meet at a point, let’s call it point \({\small M}\).
\(\\[1pt]\)

\(\\[1pt]\)
We’ll then have two similar triangles, \({\small \triangle PQU \ \sim \ \triangle PMT}\).
\(\\[1pt]\)
Since
the corresponding sides of 2 similar triangles have the same ratio,
\(\\[1pt]\)
\(\\[20pt]\hspace{2em} {\small {\large \frac{QU}{MT} \ = \ \frac{PQ}{PM} } }\)
\(\\[20pt]\hspace{2em} {\small {\large \frac{QU}{6} \ = \ \frac{5}{10} } }\)
\(\\[20pt]\hspace{2.5em} {\small QU \ = \ {\large \frac{5 \ \times \ 6}{10} } }\)
\(\hspace{2.5em} {\small QU \ = \ 3 }\)
\(\\[1pt]\)
\({\small 2.\enspace}\) Name the triangle which is similar to triangle PQR and calculate the values of the unknown lengths.
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{a}).\hspace{0.8em}}\)
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.2em}(\textrm{a}).\hspace{0.8em}}\) \({\small \triangle PQR \ \sim \ \triangle ABR}\)
\(\\[10pt]{\small\hspace{2.8em} \angle P \ = \ \angle A \ }\) (corresponding angles)
\(\\[10pt]{\small\hspace{2.8em} \angle Q \ = \ \angle B \ }\) (corresponding angles)
\(\\[10pt]{\small\hspace{2.8em} \angle R \ = \ \angle R \ }\) (same angle)
\(\\[10pt]{\small\hspace{2.5em} {\large \therefore} \enspace \triangle PQR \ \sim \ \triangle ABR \ }\) (AAA)
\(\\[1pt]\)
Since \({\small \triangle PQR \ \sim \ \triangle ABR}\),
\(\\[1pt]\)
\(\\[20pt]\hspace{2em} {\small {\large \frac{AB}{PQ} \ = \ \frac{BR}{QR} } }\)
\(\\[20pt]\hspace{3em} {\small {\large \frac{2}{6} \ = \ \frac{5}{5 \ + \ x} } }\)
\(\\[15pt]\hspace{1.8em} {\small 5 \ + \ x \ = \ 15 }\)
\(\\[15pt]\hspace{3.7em} {\small x \ = \ 10 }\)
And also,
\(\\[1pt]\)
\(\\[20pt]\hspace{2em} {\small {\large \frac{AB}{PQ} \ = \ \frac{AR}{PR} } }\)
\(\\[20pt]\hspace{3em} {\small {\large \frac{2}{6} \ = \ \frac{4}{4 \ + \ y} } }\)
\(\\[15pt]\hspace{1.8em} {\small 4 \ + \ y \ = \ 12 }\)
\(\\[25pt]\hspace{3.7em} {\small y \ = \ 8 }\)
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{b}).\hspace{0.8em}}\)
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.2em}(\textrm{b}).\hspace{0.8em}}\) \({\small \triangle PQR \ \sim \ \triangle TSR}\)
\(\\[10pt]{\small\hspace{2.8em} \angle P \ = \ \angle T \ }\) (alternate angles)
\(\\[10pt]{\small\hspace{2.8em} \angle Q \ = \ \angle S \ }\) (alternate angles)
\(\\[10pt]{\small\hspace{2.8em} \angle R \ = \ \angle R \ }\) (same angle)
\(\\[10pt]{\small\hspace{2.5em} {\large \therefore} \enspace \triangle PQR \ \sim \ \triangle TSR \ }\) (AAA)
\(\\[1pt]\)
Since \({\small \triangle PQR \ \sim \ \triangle TSR}\),
\(\\[1pt]\)
\(\\[20pt]\hspace{2em} {\small {\large \frac{PR}{TR} \ = \ \frac{PQ}{TS} } }\)
\(\\[20pt]\hspace{3em} {\small {\large \frac{5}{9} \ = \ \frac{x}{18} } }\)
\(\\[15pt]\hspace{3.3em} {\small 9x \ = \ 18 \ \times \ 5 }\)
\(\\[15pt]\hspace{3.7em} {\small x \ = \ 10 }\)
And also,
\(\\[1pt]\)
\(\\[20pt]\hspace{2em} {\small {\large \frac{PR}{TR} \ = \ \frac{QR}{SR} } }\)
\(\\[20pt]\hspace{3em} {\small {\large \frac{5}{9} \ = \ \frac{6}{y} } }\)
\(\\[15pt]\hspace{3.3em} {\small 5y \ = \ 9 \ \times \ 6 }\)
\(\\[20pt]\hspace{3.7em} {\small y \ = \ 10.8 }\)
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{c}).\hspace{0.8em}}\)
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.2em}(\textrm{c}).\hspace{0.8em}}\) \({\small \triangle AQR \ \sim \ \triangle QPR}\)
\(\\[10pt]{\small\hspace{2.3em} \angle AQR \ = \ \angle QPR \ }\) (right angles)
\(\\[10pt]{\small\hspace{2.3em} \angle QRA \ = \ \angle PRQ \ }\) (same angle)
\(\\[10pt]{\small\hspace{2.3em} \angle QAR \ = \ \angle PQR \ }\) (complement of \({\small \angle}\) R)
\(\\[10pt]{\small\hspace{2.5em} {\large \therefore} \enspace \triangle AQR \ \sim \ \triangle QPR \ }\) (AAA)
\(\\[1pt]\)
Since \({\small \triangle AQR \ \sim \ \triangle QPR}\),
\(\\[1pt]\)
\(\\[20pt]\hspace{2em} {\small {\large \frac{QR}{PR} \ = \ \frac{AR}{QR} } }\)
\(\\[20pt]\hspace{2.5em} {\small {\large \frac{15}{12} \ = \ \frac{12 \ + \ x}{15} } }\)
\(\\[15pt]\hspace{1em} {\small 144 \ + \ 12x \ = \ 225 }\)
\(\\[15pt]\hspace{3.7em} {\small 12x \ = \ 81 }\)
\(\\[15pt]\hspace{4.6em} {\small x \ = \ 6.75 }\)
And also,
\(\\[1pt]\)
\(\\[20pt]\hspace{2em} {\small {\large \frac{QR}{PR} \ = \ \frac{AQ}{QP} } }\)
\(\\[20pt]\hspace{2.5em} {\small {\large \frac{15}{12} \ = \ \frac{y}{9} } }\)
\(\\[15pt]\hspace{3em} {\small 12y \ = \ 15 \ \times \ 9 }\)
\(\\[20pt]\hspace{3.8em} {\small y \ = \ 11.25 }\)
\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{d}).\hspace{0.8em}}\)
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.2em}(\textrm{d}).\hspace{0.8em}}\) We can extend \({\small PQ}\) and \({\small AB}\) to meet at a point, let’s call it point \({\small M}\).
\(\\[1pt]\)

\(\\[1pt]\)
We’ll then have two similar triangles, \({\small \triangle ABR \ \sim \ \triangle MBQ}\).
\(\\[1pt]\)
Since
the corresponding sides of 2 similar triangles have the same ratio,
\(\\[1pt]\)
\(\\[20pt]\hspace{2em} {\small {\large \frac{BR}{BQ} \ = \ \frac{AR}{MQ} } }\)
\(\\[20pt]\hspace{2.4em} {\small {\large \frac{12}{27} \ = \ \frac{6}{6 \ + \ x} } }\)
\(\\[15pt]\hspace{1.2em} {\small 72 \ + \ 12x \ = \ 27 \ \times \ 6 }\)
\(\\[15pt]\hspace{3.6em} {\small 12x \ = \ 162 \ – \ 72 }\)
\(\\[15pt]\hspace{4.5em} {\small x \ = \ 7.5 }\)
And also,
\(\\[1pt]\)
\(\\[20pt]\hspace{2em} {\small {\large \frac{BR}{RQ} \ = \ \frac{AB}{MB} } }\)
\(\\[20pt]\hspace{2.4em} {\small {\large \frac{12}{15} \ = \ \frac{y}{10} } }\)
\(\\[15pt]\hspace{3em} {\small 15y \ = \ 12 \ \times \ 10 }\)
\(\\[20pt]\hspace{3.9em} {\small y \ = \ 8 }\)
\(\\[1pt]\)
\({\small 3.\enspace}\) In the diagram,
AB = 5 cm,
BD = 12 cm and
DE = 7 cm. Calculate
BC.
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.6em} \triangle ABC \ \sim \ \triangle CDE}\)
\(\\[10pt]{\small\hspace{2.3em} \angle ABC \ = \ \angle CDE \ }\) (right angles)
\(\\[13pt]{\small\hspace{2.3em} \angle BAC \ = \ \angle DCE \ }\)
\(\\[10pt]\) * Proof that \( {\small\angle BAC \ = \ \angle DCE }\),
\(\\[15pt]{\small\hspace{0.6em} \enspace \angle ACB \ + \ \angle ACE \ + \ \angle DCE \ = \ 180^{\large{\circ}} }\)
\(\\[15pt]{\small 90^{\large{\circ}} \ – \ \angle BAC \ + \ 90^{\large{\circ}} \ + \ \angle ECD \ = \ 180^{\large{\circ}} }\)
\(\\[15pt]{\small\hspace{0.5em} \angle DCE \ = \ 180^{\large{\circ}} \ – \ 90^{\large{\circ}} \ – \ 90^{\large{\circ}} \ + \ \angle BAC }\)
\(\\[15pt]{\small\hspace{0.5em} \angle DCE \ = \ \angle BAC }\)
\(\\[10pt]{\small\hspace{2em} {\large \therefore} \enspace \triangle ABC \ \sim \ \triangle CDE \ }\) (AAA)
\(\\[1pt]\)
Since \({\small \triangle ABC \ \sim \ \triangle CDE }\),
\(\\[1pt]\)
\(\\[20pt]\hspace{3.8em} {\small {\large \frac{AB}{CD} \ = \ \frac{BC}{DE} } }\)
\(\\[20pt]\hspace{2.2em} {\small {\large \frac{5}{12 \ – \ BC} \ = \ \frac{BC}{7} } }\)
\(\\[12pt]\hspace{1.2em}\) Let BC = x,
\(\\[20pt]\hspace{3.7em} {\small {\large \frac{5}{12 \ – \ x} \ = \ \frac{x}{7} } }\)
\(\\[15pt]\hspace{3.5em} {\small 12x \ – \ {x}^{2} \ = \ 35 }\)
\(\\[15pt]\hspace{1.2em} {\small {x}^{2} \ – \ 12x \ + \ 35 \ = \ 0 }\)
\(\\[15pt]\hspace{1.6em} {\small (x \ – \ 7)(x \ – \ 5) \ = \ 0 }\)
\(\\[15pt]\hspace{1.2em} {\small x \ = \ 7 \enspace }\) or \(\enspace {\small x \ = \ 5 }\)
\(\\[1pt]\)
\({\small 4.\enspace}\) In the diagram shown,
PQ,
LM and
RS are parallel. If
PQ = 6 cm,
RS = 10 cm, calculate the length of
LM.
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.6em} \triangle LMR \ \sim \ \triangle PQR}\)
\(\\[10pt]{\small\hspace{2.8em} \angle L \ = \ \angle P \ }\) (corresponding angles)
\(\\[10pt]{\small\hspace{2.8em} \angle M \ = \ \angle Q \ }\) (corresponding angles)
\(\\[10pt]{\small\hspace{2.8em} \angle R \ = \ \angle R \ }\) (same angle)
\(\\[10pt]{\small\hspace{2.5em} {\large \therefore} \enspace \triangle LMR \ \sim \ \triangle PQR \ }\) (AAA)
\(\\[1pt]\)
Since \({\small \triangle LMR \ \sim \ \triangle PQR}\),
\(\\[1pt]\)
\(\\[20pt]\hspace{3em} {\small {\large \frac{LM}{PQ} \ = \ \frac{LR}{PR} } }\)
\(\\[25pt]\hspace{3em} {\small {\large \frac{LM}{6} \ = \ \frac{LR}{PR} } }\)
And also,
\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.6em} \triangle PML \ \sim \ \triangle PSR}\)
\(\\[10pt]{\small\hspace{2.8em} \angle L \ = \ \angle R \ }\) (corresponding angles)
\(\\[10pt]{\small\hspace{2.8em} \angle M \ = \ \angle S \ }\) (corresponding angles)
\(\\[10pt]{\small\hspace{2.8em} \angle P \ = \ \angle P \ }\) (same angle)
\(\\[10pt]{\small\hspace{2.5em} {\large \therefore} \enspace \triangle PML \ \sim \ \triangle PSR \ }\) (AAA)
\(\\[1pt]\)
Since \({\small \triangle PML \ \sim \ \triangle PSR}\),
\(\\[1pt]\)
\(\\[20pt]\hspace{4em} {\small {\large \frac{LM}{RS} \ = \ \frac{PL}{PR} } }\)
\(\\[25pt]\hspace{4em} {\small {\large \frac{LM}{10} \ = \ \frac{PL}{PR} } }\)
Hence,
\(\\[1pt]\)
\(\\[20pt]\hspace{5.3em} {\small {\large \frac{PR}{PR}} \ = \ 1 }\)
\(\\[20pt]\hspace{3em} {\small {\large \frac{PL \ + \ LR}{PR}} \ = \ 1 }\)
\(\\[20pt]\hspace{2.3em} {\small {\large \frac{PL}{PR}} \ + \ {\large \frac{LR}{PR}} \ = \ 1 }\)
\(\\[20pt]\hspace{2em} {\small {\large \frac{LM}{10}} \ + \ {\large \frac{LM}{6}} \ = \ 1 }\)
\(\\[20pt]\hspace{4.4em} {\small {\large \frac{4}{15}} LM \ = \ 1 }\)
\(\\[20pt]\hspace{5.7em} {\small LM \ = \ {\large\frac{15}{4} } }\)
\(\hspace{5.7em} {\small LM \ = \ 3.75 } \)
\(\\[1pt]\)
\({\small 5.\enspace}\) Given that \({\small \triangle AED}\) and \({\small \triangle BEC}\) are isosceles triangles, prove that \({\small \triangle ABE}\) and \({\small \triangle EDC}\) are congruent.
\(\\[1pt]\)

\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.6em} \triangle ABE \ \sim \ \triangle DCE}\)
\(\\[10pt]{\small\hspace{2.8em} \angle EAB \ = \ \angle EDC }\)
\(\\[10pt] \enspace\)(same angles of \({\small \triangle AED}\) )
\(\\[10pt]{\small\hspace{2.8em} \angle ABE \ = \ \angle DCE }\)
\(\\[10pt] \enspace\)(same supplement angles of \({\small \triangle BEC}\) )
\(\\[10pt]{\small\hspace{3.3em} BE \ = \ CE }\)
\(\\[10pt] \enspace\)(equal side lengths)
\(\\[20pt]{\small\hspace{2.5em} {\large \therefore} \enspace \triangle ABE \ \sim \ \triangle DCE \ }\)
(AAS)

\(\\[1pt]\)
\(\\[1pt]\)
PRACTICE MORE WITH THESE QUESTIONS BELOW!
\({\small 1.\enspace}\) In the diagram, \({\small AG \parallel BE \ }\) and \({\small CG \parallel DE}\), \({\small AB \ = \ CD \ = \ 10 \ }\) cm and \({\small BC \ = \ 5 \ }\) cm.
\(\\[1pt]\)

\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{a}).\hspace{0.8em}}\) Name a pair of congruent triangles.
\({\small\hspace{1.2em}(\textrm{b}).\hspace{0.8em}}\) Show that the triangles in (a) are congruent.
\({\small\hspace{1.2em}(\textrm{c}).\hspace{0.8em}}\) Name one triangle that is similar to \({\small \triangle BCF}\).
\({\small\hspace{1.2em}(\textrm{d}).\hspace{0.8em}}\) If \({\small DE \ = \ 6 \ }\) cm, find If \({\small CF }\).
\({\small 2. \enspace}\) In the diagram, ABCD is a quadrilateral. Point X is the intersection of AC and BD. AX = XC and BX = DX.
\(\\[1pt]\)

\(\\[1pt]\)
\({\small\hspace{1.2em}(\textrm{a}).\hspace{0.8em}}\) Name a pair of congruent triangles.
\({\small\hspace{1.2em}(\textrm{b}).\hspace{0.8em}}\) Prove that the pair in (a) is congruent.
\({\small\hspace{1.2em}(\textrm{c}).\hspace{0.8em}}\) What is the name given to the quadrilateral ABCD? Explain your answer.
\({\small 3. \enspace}\) Are the triangles below congruent? Explain your answer.
\(\\[1pt]\)

\(\\[1pt]\)
\({\small 4. \enspace}\) ABCD is a parallelogram. M is the midpoint of AB and N is the point of intersection betweeen BD and MC.
\(\\[1pt]\)

\(\\[1pt]\)
\({\small\hspace{1.2em} (\textrm{a}).\hspace{0.8em}}\) Name a triangle which is similar to \({\small \triangle MNB }\) and show that they are similar.
\({\small\hspace{1.2em} (\textrm{b}).\hspace{0.8em}}\) Find \({\small {\large \frac{MB}{DC} } }\).
\({\small\hspace{1.2em} (\textrm{c}).\hspace{0.8em}}\) Find area of \({\small \triangle DNC }\) : area of \({\small \triangle BNM }\).
\({\small 5. \enspace}\) In the diagram, PR = QS, QO = PO and \({\small \angle PSQ \ = \ 32^{\large{\circ}}}\).
\(\\[1pt]\)

\(\\[1pt]\)
\({\small\hspace{1.2em} (\textrm{a}).\hspace{0.8em}}\) Show that \({\small \triangle POS }\) and QOR are congruent, stating your reasons clearly.
\({\small\hspace{1.2em} (\textrm{b}).\hspace{0.8em}}\) Name another pair of congruent triangles.
\({\small 6. \enspace}\) In the diagram, AD is parallel to BC. AD = 9 cm, BC = 15 cm, EC = 8 cm and DC = 7 cm.
\(\\[1pt]\)

\(\\[1pt]\)
\({\small\hspace{1.2em} (\textrm{a}).\hspace{0.8em}}\) Prove that \({\small \triangle ADE }\) is similar to \({\small \triangle CBE }\).
\({\small\hspace{1.2em} (\textrm{b}).\hspace{0.8em}}\) Calculate the length of AE.
\({\small\hspace{1.2em} (\textrm{c}).\hspace{0.8em}}\) Calculate the ratio of \({\small {\large \frac{\textrm{Area of} \ \triangle ADE}{\textrm{Area of} \ \triangle ADC} }}\).
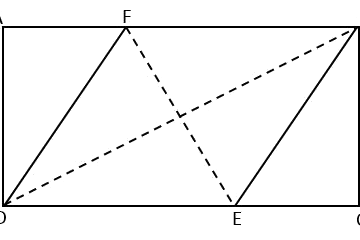
\({\small 7. \enspace}\) ABCD is a rectangle. M is the midpoint of AB and N is a point on CD. MC and BN meet at X.
\(\\[1pt]\)

\(\\[1pt]\)
\({\small\hspace{1.2em} (\textrm{a}).\hspace{0.8em}}\) Prove that \({\small \triangle CXN }\) and \({\small \triangle MXB }\) are similar.
\({\small\hspace{1.2em} (\textrm{b}).\hspace{0.8em}}\) Given that the ratio of the area of \({\small \triangle CXN }\) and \({\small \triangle MXB }\) is 9 : 4. Find the following ratios
\({\small\hspace{2.8em}(\textrm{i}).\hspace{0.7em}}\) CN : MB,
\({\small\hspace{2.8em}(\textrm{ii}).\hspace{0.7em}}\) CN : ND,
\({\small\hspace{2.8em}(\textrm{iii}).\hspace{0.5em}}\) area of \({\small \triangle BXC }\) : area of \({\small \triangle BXM }\).
\({\small 8. \enspace}\) In the diagram, ABCD is a rectangle and DEFG is a square. AEB and BCG are straight lines. Show that \({\small \angle ADE \ }\) is equal to \({\small \angle CDG}\) .
\(\\[1pt]\)

\(\\[1pt]\)
As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .
Where are the other important definitions of math topics like these.
An example of a pair of similar triangles that are also congruent
Comment teach me step by step guard