Ratio and Proportion
Ratio is used to measure the quantity of an object in terms of the other object(s).
In the olden days you may have to trade in the barter sytem.
Or, you are going on a holiday and you need to exchange your currency to another country’s currency.
Or even when you are going to make a cake and need to mix a variety of ingredients.
These are some of the examples of which a good basic knowledge on mathematical ratio might really help you.
At least you wouldn’t want your cake to taste awful, would you? =) .
Ratio can be expressed by either a colon or as a fraction between the two quantities you want to compare.
Let’s see the example below:
\(\hspace{2em} A \enspace : \enspace B \enspace = \enspace 2 \enspace : \enspace 5\)
\(\hspace{4.2em} {\large \frac{A}{B} \enspace= \enspace \frac{2}{5} }\)
The ratio of A to B is “2 to 5”.
Meanwhile in proportion, to increase or decrease the ratio by the same amount we multiply the ratio by the same number.
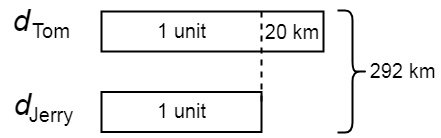
For example, if Andy has a bag consists of ten candies, how many candies would there be in 5 bags?
Therefore,
Or we can calculate the proportion of the ratio between the bags and candies,
There are 50 candies in 5 bags.
Just remember, there are a few things to keep in mind:
– To simplify a ratio expression, you can use the HCF (highest common factor) to divide both numbers in the ratio.
– More often than not, it is generally helpful to sketch the diagram and solve the questions by using the box method/unitary method/the bar model.
– Sometimes it is easier to solve the problem by writing the ratio in fractions.
– If you need to compare more than 2 quantities, find the LCM (least common multiple) of the same quantity that is being compared.
Try some of the examples below and if you need any help, just look at the solution I have written. Cheers ! =) .
\(\\[1pt]\)
EXAMPLE:
\(\\[1pt]\)
\(\hspace{2.5em} 3 \enspace : \enspace 5 \enspace = \enspace {\large \square } \enspace : \enspace 30 \)
\(\\[1pt]\)
\({\small 2.\enspace}\) Jennifer has 18 stamps. She has 10 more stamps than Isabelle. Find the ratio of the number of stamps Jennifer has to the number of stamps Isabelle has.
\(\\[1pt]\)
\({\small 3.\enspace}\) The ratio of the number of men to the number of women working in a factory is 5 : 2. There are 105 workers in the factory. How many men are working in the factory?
\(\\[1pt]\)
\({\small 4.\enspace}\) At a party, there were 8 women to every 15 men. 35 more men than women attended the party. How many women were there at the party?
\(\\[1pt]\)
\({\small 5.\enspace}\) The ratio of A : B is 2 : 5. The ratio of B : C is 7 : 4. Find the ratio of A : B : C.
\(\\[1pt]\)
\({\small 6.\enspace}\) The ratio of the number of boys to the number of girls at a workshop was 5 : 6. After 22 boys left the workshop, the ratio of the number of boys to the number of girls who remained became 2 : 3. Find the total number of students who attended the workshop at first.
\(\\[1pt]\)
\({\small 7.\enspace}\) The ratio of Uncle Gary’s age to his son’s age now is 5 : 2. Given that the ratio of the their ages 10 years ago is 5 : 1, find Uncle Gary’s age now.
\(\\[1pt]\)
\({\small 8.\enspace}\) The ratio of the number of tennis balls in Basket A to the number of tennis balls in Basket B was 5 : 4. When 8 tennis balls were taken out from Basket A and placed into Basket B, there was an equal number of tennis balls in each basket. How many tennis balls were there in Basket A at first?
\(\\[1pt]\)
\({\small 9.\enspace}\) At a swimming carnival, the ratio of the number of swimmers to the number of non-swimmers is 8 : 9. The ratio of the number of female swimmers to the number of male swimmers is 4 : 7. If \({\small {\large \frac{2}{3}} }\) of the non-swimmers are females and there are 64 female swimmers, how many male and female non-swimmers are there at the swimming carnival?
\(\\[1pt]\)
\({\small 10.\enspace}\) Elisa, John and Wilson donated a sum of money to the school building fund. Elisa donated \({\small {\large \frac{3}{10}} }\) of the money. The remaining was donated by John and Wilson in the ratio 5 : 9. Elisa donated $900 less than Wilson.
\({\small\hspace{1.2em}(\textrm{a}).\hspace{0.8em}}\) How much did John donate?
\({\small\hspace{1.2em}(\textrm{b}).\hspace{0.8em}}\) For every one dollar donated by Elisa, how much did Wilson donate?
\(\\[1pt]\)
PRACTICE MORE WITH THESE QUESTIONS BELOW!
\({\small 1.\enspace}\) The ratio of the number sweets Alfred had to the number of sweets Brandon had was 3 : 8. After each of them received 45 sweets, the ratio of the number sweets Alfred had to the number of sweets Brandon had became 3 : 5. How many sweets did they have altogether at first?
\({\small 2. \enspace}\) The length and breadth of a rectangle are in the ratio 7 : 4. Given that the perimeter of the rectangle is 352 cm, find its area.
\({\small 3. \enspace}\) John’s present age to Andrew’s present age is 3 : 1. In 6 years’ time, the ratio of John’s age to Andrew’s age will be 5 : 2. What is John’s present age?
\({\small 4. \enspace}\) Grace and Alice have some beads in the ratio 9 : 5. Grace gave 28 of her beads to her sister and Alice bought another 32 beads. At the end, Grace and Alice have the same number of beads. How many beads did they have altogether at first?
\({\small 5. \enspace}\) Greg went shopping with $360. He bought some calculators and shirts and had $8.50 left. Each shirt cost $15.50 more than a calculator. He bought 3 fewer calculators than shirts. How many shirts and calculators did he buy if each calculator cost $17.50?
\({\small 6. \enspace}\) When Belinda purchased 6 kg of rice, she was short of $6. When she purchased 8 kg of the same type of rice, she was short of $14. How much money did she have?
\({\small 7. \enspace}\) If Liming gives Dave $8, both of them will have the same amount of money. If Florence adds $14 to Liming’s original sum of money, the ratio of Liming’s money to Dave’s original sum of money will be 5 : 2. How much has Liming at first?
\({\small 8. \enspace}\) Peter, Cecilia and Tony have a certain number of books. If Peter gives 6 books to Cecilia, he will have half as many books as she. If Tony gives 10 books to Cecilia, both of them will have the same number of books. If Cecilia has 30 books at first, how many books do Peter and Tony have altogether at the beginning?
\({\small 9. \enspace}\) Joanne and Bernard had a certain number of stamps each. If Joanne gave 90 stamps to Bernard, they would have the same number of stamps. If Bernard gave 10 stamps to Joanne, she would have 5 times as many stamps as Bernard. How many stamsps did Joanne have at first?
\({\small 10.\enspace}\) A group of boys played only two games. \({\small {\large \frac{1}{3}} }\) of them played basketball and \({\small {\large \frac{1}{4}} }\) of them played football. \({\small {\large \frac{1}{6}} }\) of them played both games and 56 boys did not play any games at all. How many boys were there?
\(\\[1pt]\)
As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .