Parametric Equations
The traditional representation of y as a function of x or \({\small y = f(x)}\) is inadequate to represent a curve or a surface.
To be able to draw a curve or a surface, we need to separate the x and y and write them in terms of an independent variable.
Parametric equations are used to express the Cartesian coordinates (x and y) in terms of another independent variable, usually named as t.
The typical procedure in this topic is to find the gradient of the curve or \({ \large\frac{\mathrm{d}y}{\mathrm{d}x} }\). We can do this by finding each derivative of x and y with respect to t and then divide them both.
Let’s dig into some of the examples to show you what I mean. Cheers ! =) .
\(\\[1pt]\)
EXAMPLE:
\({\small 1.\enspace}\) The parametric equations of a curve are
\(\\[1pt]\)
\(\hspace{3em} x = {\large \frac{1}{{\cos}^{3}t}}, \quad y = {\tan}^{3}t\).
\(\\[1pt]\)
where \(0 \ \le \ t \ \le \ \frac{\pi}{2}\)
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(a\right). \enspace }\) Show that \( {\large\frac{\mathrm{d}y}{\mathrm{d}x} } = \sin \ t\)
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(b\right). \enspace }\) Hence, show that the equation of the tangent to the curve at the point with parameter
t is \( y = x \sin t \ – \ \tan t\).
\(\hspace{1.2em} {\large\frac{\mathrm{d}y}{\mathrm{d}x} } = {\large\frac{\mathrm{d}y}{\mathrm{d}t} } \ \div \ {\large\frac{\mathrm{d}x}{\mathrm{d}t} }\)
\(\\[1pt]\)
\({\small\hspace{0.3em}\left(a\right). \hspace{0.3em} }\) So, we’ll need to calculate \({\small {\large\frac{\mathrm{d}y}{\mathrm{d}t} }}\) and \({\small{\large\frac{\mathrm{d}x}{\mathrm{d}t} }}\)
\(\\[1pt]\)
\(\\[15pt]\hspace{1.2em} {\large\frac{\mathrm{d}y}{\mathrm{d}t} }\)
\(\\[15pt]\hspace{1.2em} = \ {\large\frac{\mathrm{d} \ ({\tan}^{3}t)}{\mathrm{d}t} } \)
\(\\[15pt]\hspace{1.2em} = \ 3 \ {\tan}^{2} t \ {\large\frac{\mathrm{d} \ (\tan \ t)}{\mathrm{d}t} } \)
\(\\[20pt]\hspace{1.2em} = \ 3 \ {\tan}^{2} t \ {\sec}^{2} t \)
\(\\[15pt]\hspace{1.2em} {\large\frac{\mathrm{d}x}{\mathrm{d}t} }\)
\(\\[15pt]\hspace{1.2em} = \ {\large\frac{\mathrm{d} \ ({\cos}^{-3}t)}{\mathrm{d}t} } \)
\(\\[15pt]\hspace{1.2em} = \ (-3) \ {\cos}^{-4} t \ {\large\frac{\mathrm{d} \ ({\cos} \ t)}{\mathrm{d}t} } \)
\(\\[15pt]\hspace{1.2em} = \ (-3) \ {\large\frac{-\sin t}{{\cos}^{4} \ t} } \)
\(\\[25pt]\hspace{1.2em} = \ {\large\frac{3\sin t}{{\cos}^{4} \ t} } \)
\(\\[15pt]\hspace{1.2em} {\large\frac{\mathrm{d}y}{\mathrm{d}x} } = {\large\frac{\mathrm{d}y}{\mathrm{d}t} } \ \div \ {\large\frac{\mathrm{d}x}{\mathrm{d}t} }\)
\(\\[25pt]\hspace{1.2em} = \ 3 \ {\tan}^{2} t \ {\sec}^{2} t \ \div \ {\large\frac{3\sin t}{{\cos}^{4} \ t} } \)
\(\\[25pt]\hspace{1.2em} = \ {\large \frac{3 \ {\tan}^{2} t \ {\sec}^{2} t \ {\cos}^{4} t }{3 \sin \ t} } \)
\(\\[25pt]\hspace{1.2em} = \ \require{cancel} {\large \frac{\cancel{3} \ {\sin}^{2} t \ \cancel{{\cos}^{4} t} }{\cancel{3} \ \cancel{{\cos}^{2} t} \ \cancel{{\cos}^{2} t} \ \sin \ t} } \)
\(\\[15pt]\hspace{1.2em} = \ {\large \frac{ {\sin}^{2} t }{ \sin \ t} } \)
\(\\[25pt]\hspace{1.2em} = \ \sin \ t \)
\({\small\hspace{1.2em}\left(b\right). \enspace }\) The line equation can be written as follows:
\(\\[1pt]\)
\(\\[10pt]\hspace{3em} y \ – \ y_{1} \ = \ m(x \ – \ x_{1}) \)
\(\\[7pt]\hspace{1.2em} (x_{1}, \ y_{1})\) is a coordinate on the line,
\(\\[12pt]\hspace{2.3em} m \hspace{1.4em}\) is the gradient of the line.
\(\\[7pt]\hspace{1.2em}\) Hence, we substitute \((x_{1}\) & \(y_{1})\) with our parametric equations, x and y as a function of t. Also, the gradient, m is simply “the rate of change” or \({ \large\frac{\mathrm{d}y}{\mathrm{d}x} }\) we have calculated in part (a).
\(\\[1pt]\)
\(\\[10pt]\hspace{2.1em} y \ – \ {\tan}^{3}t \ = \ \sin t \ (x \ – \ {\cos}^{-3} t) \)
\(\\[10pt]\hspace{2.1em} y \ = \ x \ \sin t \ – \ \sin t \times {\cos}^{-3} t \ + \ {\tan}^{3}t \)
\(\\[10pt]\hspace{2.1em} y \ = \ x \ \sin t \ – \ \tan t \times {\sec}^{2} t \ + \ {\tan}^{3}t \)
\(\\[10pt]\hspace{2.1em} y \ = \ x \ \sin t \ – \ \tan t \ ({\sec}^{2} t \ – \ {\tan}^{2} t )\)
\(\\[7pt]\hspace{1.2em}\) Note that \( ({\sec}^{2} t \ – \ {\tan}^{2} t) \ = \ 1\). Thus,
\(\\[10pt]\hspace{2.1em} y \ = \ x \ \sin t \ – \ \tan t \)
\(\\[1pt]\)
\({\small 2.\enspace}\) The parametric equations of a curve are
\(\\[1pt]\)
\(\hspace{3em} x = e^{-t} \cos t, \quad y = e^{-t} \sin t\).
\(\\[1pt]\)
Show that \( {\large\frac{\mathrm{d}y}{\mathrm{d}x} } = \tan \big(t \ – \ {\large\frac{\pi}{4}}\big)\)
\(\hspace{1.2em} {\large\frac{\mathrm{d}y}{\mathrm{d}x} } = {\large\frac{\mathrm{d}y}{\mathrm{d}t} } \ \div \ {\large\frac{\mathrm{d}x}{\mathrm{d}t} }\)
\(\\[1pt]\)
\(\\[10pt]\hspace{1.2em} {\large\frac{\mathrm{d}y}{\mathrm{d}t} }\)
\(\\[10pt]\hspace{1.2em} = \ – e^{-t} \ \sin t \ + \ e^{-t} \ \cos t \)
\(\\[15pt]\hspace{1.2em} = \ e^{-t} \ (\cos t \ – \ \sin t) \)
\(\\[10pt]\hspace{1.2em} {\large\frac{\mathrm{d}x}{\mathrm{d}t} }\)
\(\\[10pt]\hspace{1.2em} = \ – e^{-t} \ \cos t \ – \ e^{-t} \ \sin t \)
\(\\[15pt]\hspace{1.2em} = \ – e^{-t} \ (\cos t \ + \ \sin t) \)
\(\\[15pt]\hspace{1.2em} {\large\frac{\mathrm{d}y}{\mathrm{d}x} } = {\large\frac{\mathrm{d}y}{\mathrm{d}t} } \ \div \ {\large\frac{\mathrm{d}x}{\mathrm{d}t} }\)
\(\\[25pt]\hspace{1.2em} = \ \require{cancel} {\large \frac{\cancel{e^{-t}} \ (\cos t \ – \ \sin t) }{- \ \cancel{e^{-t}} \ (\cos t \ + \ \sin t)}}\)
\(\\[25pt]\hspace{1.2em} = \ {\large \frac{ (\cos t \ – \ \sin t) }{- \ (\cos t \ + \ \sin t)}}\)
\(\\[25pt]\hspace{1.2em} = \ {\large \frac{ – \ (\cos t \ – \ \sin t) }{(\cos t \ + \ \sin t)}}\)
\(\\[25pt]\hspace{1.2em} = \ {\large \frac{ \sin t \ – \ \cos t }{\cos t \ + \ \sin t}}\)
\(\hspace{1.2em}\) Divide the numerator and denominator by \({\small \cos t }\),
\(\\[1pt]\)
\(\\[25pt]\hspace{1.2em} = \ {\large \frac{ \tan t \ – \ 1 }{ 1 \ + \ \tan t}}\)
\(\hspace{1.2em}\) Since \({\small \tan {\large\frac{\pi}{4}} \ = 1 }\),
\(\\[1pt]\)
\(\\[25pt]\hspace{1.2em} = \ {\large \frac{ \tan t \ – \ 1 }{ 1 \ + \ \tan t \ \times 1}}\)
\(\\[25pt]\hspace{1.2em} = \ {\large \frac{ \tan t \ – \ \tan {\large\frac{\pi}{4}} }{ 1 \ + \ \tan t \ \times \tan {\large\frac{\pi}{4}}}}\)
\(\hspace{1.2em} = \ \tan \big(t \ – \ {\large\frac{\pi}{4}}\big) \)
\(\\[1pt]\)
\({\small 3.\enspace}\) The parametric equations of a curve are
\(\\[1pt]\)
\(\hspace{3em} x = \ln (2t \ + \ 3), \quad y = { \large\frac{3t \ + \ 2}{2t \ + \ 3} }\).
\(\\[1pt]\)
Find the gradient of the curve at the point where it crosses the
y-axis.
\(\hspace{1.2em} {\large\frac{\mathrm{d}y}{\mathrm{d}x} } = {\large\frac{\mathrm{d}y}{\mathrm{d}t} } \ \div \ {\large\frac{\mathrm{d}x}{\mathrm{d}t} }\)
\(\\[1pt]\)
\(\hspace{1.2em}\) To find \({\large\frac{\mathrm{d}y}{\mathrm{d}t} }\), we will use the Quotient Rule,
\(\\[1pt]\)
\(\\[25pt]\hspace{1.2em} \frac{\mathrm{d}}{\mathrm{d}t}\left( {\Large\frac{u}{v}} \right) = \frac{ {\Large\frac{\mathrm{d}u}{\mathrm{d}t}}v \ – \ u{\Large\frac{\mathrm{d}v}{\mathrm{d}t}}}{v^2} \)
\(\\[10pt]\hspace{1.2em}\) Let \({\small u \ = \ 3t \ + \ 2 }\)
\(\\[10pt]\hspace{2em} \frac{\mathrm{d}u}{\mathrm{d}t} \ = \ 3 \)
\(\\[10pt]\hspace{1.2em}\) Let \({\small v \ = \ 2t \ + \ 3 }\)
\(\\[20pt]\hspace{2em} \frac{\mathrm{d}v}{\mathrm{d}t} \ = \ 2 \)
\(\\[20pt]\hspace{1.2em} {\large\frac{\mathrm{d}y}{\mathrm{d}t}} \ = \ {\large\frac{3(2t \ + \ 3) \ – \ 2(3t \ + \ 2)}{(2t \ + \ 3)^{2}}}\)
\(\\[20pt]\hspace{1.2em} {\large\frac{\mathrm{d}y}{\mathrm{d}t}} \ = \ {\large\frac{6t \ + \ 9 \ – \ 6t \ – \ 4}{(2t \ + \ 3)^{2}}}\)
\(\\[25pt]\hspace{1.2em} {\large\frac{\mathrm{d}y}{\mathrm{d}t}} \ = \ {\large\frac{5}{(2t \ + \ 3)^{2}}}\)
\(\\[20pt]\hspace{1.2em} {\large\frac{\mathrm{d}x}{\mathrm{d}t} }\)
\(\\[20pt]\hspace{1.2em} = \ {\large \frac{1}{(2t \ + \ 3)}}\frac{\mathrm{d}}{\mathrm{d}t}(2t \ + \ 3) \)
\(\\[30pt]\hspace{1.2em} = \ {\large \frac{2}{(2t \ + \ 3)}} \)
\(\\[20pt]\hspace{1.2em} {\large\frac{\mathrm{d}y}{\mathrm{d}x} } = \ {\large\frac{\mathrm{d}y}{\mathrm{d}t} } \ \div \ {\large\frac{\mathrm{d}x}{\mathrm{d}t} }\)
\(\\[20pt]\hspace{1.2em} = \ {\large\frac{5}{(2t \ + \ 3)^{2}}} \ \div \ {\large \frac{2}{(2t \ + \ 3)}} \)
\(\\[20pt]\hspace{1.2em} = \ \require{cancel} {\large\frac{5\cancel{(2t \ + \ 3)}}{2(2t \ + \ 3)^{\cancel{2}}}} \)
\(\\[30pt]\hspace{1.2em} = \ {\large\frac{5}{2(2t \ + \ 3)}} \)
\(\hspace{1.2em}\) The point where it crosses the y-axis,
\(\\[1pt]\)
\(\\[10pt]\hspace{1.2em} x \ = \ 0\)
\(\\[10pt]\hspace{1.2em} 0 = \ \ln (2t \ + \ 3)\)
\(\\[10pt]\hspace{1.2em} 2t \ + \ 3 \ = \ 1\)
\(\\[10pt]\hspace{1.2em} t \ = \ -1\)
\(\hspace{1.2em}\) Substitute \({\small t \ = \ -1 \ }\) to the gradient or \(\frac{\mathrm{d}y}{\mathrm{d}x}\),
\(\\[1pt]\)
\(\\[20pt]\hspace{1.2em} = \ {\large\frac{5}{2 \ (2(1) \ + \ 3)}} \)
\(\hspace{1.2em} = \ 1 \)
\(\\[1pt]\)
\({\small 4.\enspace}\) The parametric equations of a curve are
\(\\[1pt]\)
\(\hspace{1.2em} {\small x = \ 2\sin \theta \ + \ \sin 2\theta, \enspace y = \ 2\cos \theta \ + \ \cos 2\theta }\),
\(\\[1pt]\)
where \(0 \ \lt \ \theta \ \lt \ \pi\).
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(\textrm{i}\right). \enspace }\) Obtain an expression for \( {\small {\large\frac{\mathrm{d}y}{\mathrm{d}x} } }\) in terms of \({\small \theta }\).
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(\textrm{ii}\right). \enspace }\) Hence find the exact coordinates of the point on the curve at which the tangent is parallel to the
y-axis.
\(\hspace{1.2em} {\small{\large\frac{\mathrm{d}y}{\mathrm{d}x} } \ = \ {\large\frac{\mathrm{d}y}{\mathrm{d} \theta} } \ \div \ {\large\frac{\mathrm{d}x}{\mathrm{d} \theta} }}\)
\(\\[1pt]\)
\({\small\hspace{0.5em}\left(\textrm{i}\right). \hspace{0.3em} }\) So, we’ll calculate \({\small {\large\frac{\mathrm{d}y}{\mathrm{d} \theta} }}\) and \({\small{\large\frac{\mathrm{d}x}{\mathrm{d} \theta} }}\)
\(\\[1pt]\)
\(\\[15pt]\hspace{1.2em} {\small{\large\frac{\mathrm{d}y}{\mathrm{d} \theta} } }\)
\(\\[15pt]\hspace{1.2em} = \ {\small {\large\frac{\mathrm{d} \ (2\cos \theta \ + \ \cos 2\theta)}{\mathrm{d} \theta} } } \)
\(\\[15pt]\hspace{1.2em} = \ {\small 2{\large\frac{\mathrm{d} \cos \theta}{\mathrm{d} \theta} } \ – \ \sin 2\theta {\large\frac{\mathrm{d} (2\theta)}{\mathrm{d} \theta}} }\)
\(\\[20pt]\hspace{1.2em} = \ {\small -2 \ \sin \theta \ – \ 2 \ \sin 2 \theta }\)
\(\\[15pt]\hspace{1.2em} {\small {\large\frac{\mathrm{d}x}{\mathrm{d} \theta} } }\)
\(\\[15pt]\hspace{1.2em} = \ {\small {\large\frac{\mathrm{d} \ (2\sin \theta \ + \ \sin 2\theta)}{\mathrm{d} \theta} } } \)
\(\\[15pt]\hspace{1.2em} = \ {\small 2{\large\frac{\mathrm{d} \sin \theta}{\mathrm{d} \theta} } \ + \ \cos 2\theta {\large\frac{\mathrm{d} (2\theta)}{\mathrm{d} \theta}} }\)
\(\\[20pt]\hspace{1.2em} = \ {\small 2 \ \cos \theta \ + \ 2 \ \cos 2 \theta }\)
\(\\[25pt]\hspace{1.2em} {\small {\large\frac{\mathrm{d}y}{\mathrm{d}x} } = {\large\frac{\mathrm{d}y}{\mathrm{d} \theta} } \ \div \ {\large\frac{\mathrm{d}x}{\mathrm{d} \theta} }}\)
\(\\[20pt]\hspace{1.2em} = \ {\small {\large \frac{-2 \ \sin \theta \ – \ 2 \ \sin 2 \theta }{2 \ \cos \theta \ + \ 2 \ \cos 2 \theta} } }\)
\(\\[30pt]\hspace{1.2em} = \ {\small {\large \frac{- \ \sin \theta \ – \ \sin 2 \theta }{ \cos \theta \ + \ \cos 2 \theta} } }\)
\({\small\hspace{1.2em}\left(\textrm{ii}\right). \enspace }\) The tangent is parallel to the y-axis when the gradient or \( {\small {\large\frac{\mathrm{d}y}{\mathrm{d}x} } }\) is undefined.
\(\\[1pt]\)
It can be found by equating the denominator term of \( {\small {\large\frac{\mathrm{d}y}{\mathrm{d}x} } }\) to zero.
\(\\[1pt]\)
\(\\[7pt]\) Using the result in part (i),
\(\\[12pt]\hspace{1.2em} {\small \cos \theta \ + \ \cos 2 \theta \ = \ 0 }\)
\(\\[7pt]\) Applying double angle formula to \({\small \cos 2\theta}\),
\(\\[12pt]\hspace{1.2em} {\small \cos \theta \ + \ 2{\cos}^{2} \theta \ – \ 1 \ = \ 0 }\)
\(\\[12pt]\hspace{1.2em} {\small 2{\cos}^{2} \theta \ + \ \cos \theta \ – \ 1 \ = \ 0 }\)
\(\\[12pt]\hspace{1.2em} {\small (2\cos \theta \ – \ 1) (\cos \theta \ + \ 1) \ = \ 0 }\)
\(\\[12pt]\hspace{1.2em} {\small (2\cos \theta \ – \ 1) \ = \ 0 \ \ \textrm{or} \ \ (\cos \theta \ + \ 1) \ = \ 0 }\)
\(\\[15pt]\hspace{1.2em} {\small \cos \theta \ = \ {\large\frac{1}{2}} }\)
\(\\[15pt]\hspace{2.5em} {\small \theta \ = \ {\large\frac{\pi}{3}} }\)
The other solution for \({\small (\cos \theta \ + \ 1) \ = \ 0 }\) is not included because it is outside the domain of \({\small \theta }\) where \(0 \ \lt \ \theta \ \lt \ \pi\).
\(\\[1pt]\)
Then, we substitute \({\small \theta \ = \ {\large\frac{\pi}{3}} }\) to find the coordinates of the point,
\(\\[1pt]\)
\(\\[12pt]\hspace{1.2em} {\small x \ = \ 2\sin {\large\frac{\pi}{3}} \ + \ \sin {\large\frac{2\pi}{3}} }\)
\(\\[15pt]\hspace{2.2em} {\small = \ 2 ( {\large\frac{1}{2}}\sqrt{3} ) \ + \ {\large\frac{1}{2}}\sqrt{3} }\)
\(\\[20pt]\hspace{2.2em} {\small = \ {\large\frac{3}{2}}\sqrt{3} }\)
\(\\[12pt]\hspace{1.2em} {\small y \ = \ 2\cos {\large\frac{\pi}{3}} \ + \ \cos {\large\frac{2\pi}{3}} }\)
\(\\[15pt]\hspace{2.2em} {\small = \ 2 ( {\large\frac{1}{2}} ) \ – \ {\large\frac{1}{2}} }\)
\(\\[15pt]\hspace{2.2em} {\small = \ {\large\frac{1}{2}} }\)
The coordinates are \({\small ( {\large\frac{3}{2}}\sqrt{3}, \ {\large\frac{1}{2}} )}\).
\(\\[1pt]\)
\({\small 5.\enspace}\) The parametric equations of a curve are
\(\\[1pt]\)
\(\hspace{1.2em} x = \ 2 t \ + \sin 2t, \enspace y = \ 1 \ – \ 2\cos 2t \),
\(\\[1pt]\)
where \(-\frac{1}{2}\pi \ \lt \ t \ \lt \ \frac{1}{2}\pi\).
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(\textrm{i}\right). \enspace }\) Show that \( {\small {\large\frac{\mathrm{d}y}{\mathrm{d}x} } \ = \ 2 \tan t }\).
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(\textrm{ii}\right). \enspace }\) Hence find the
x-coordinate of the point on the curve at which the gradient of the normal is 2. Give your answer correct to 3 significant figures.
\(\hspace{1.2em} {\small{\large\frac{\mathrm{d}y}{\mathrm{d}x} } \ = \ {\large\frac{\mathrm{d}y}{\mathrm{d} t} } \ \div \ {\large\frac{\mathrm{d}x}{\mathrm{d} t} }}\)
\(\\[1pt]\)
\({\small\hspace{0.5em}\left(\textrm{i}\right). \hspace{0.3em} }\) So, we’ll calculate \({\small {\large\frac{\mathrm{d}y}{\mathrm{d} t} }}\) and \({\small{\large\frac{\mathrm{d}x}{\mathrm{d} t} }}\)
\(\\[1pt]\)
\(\\[15pt]\hspace{1.2em} {\small{\large\frac{\mathrm{d}y}{\mathrm{d} t} } }\)
\(\\[15pt]\hspace{1.2em} = \ {\small {\large\frac{\mathrm{d} \ (1 \ – \ 2\cos 2t)}{\mathrm{d} t} } } \)
\(\\[15pt]\hspace{1.2em} = \ {\small (-2) \ (-\sin 2t) {\large\frac{\mathrm{d} (2t)}{\mathrm{d} t}} }\)
\(\\[20pt]\hspace{1.2em} = \ {\small 4 \ \sin 2 t }\)
\(\\[15pt]\hspace{1.2em} {\small {\large\frac{\mathrm{d}x}{\mathrm{d} t} } }\)
\(\\[15pt]\hspace{1.2em} = \ {\small {\large\frac{\mathrm{d} \ (2t \ + \ \sin 2t)}{\mathrm{d}t} } } \)
\(\\[15pt]\hspace{1.2em} = \ {\small 2 \ + \ \cos 2t {\large\frac{\mathrm{d} (2t)}{\mathrm{d}t}} }\)
\(\\[20pt]\hspace{1.2em} = \ {\small 2 \ + \ 2 \ \cos 2t }\)
\(\\[15pt]\hspace{1.2em} {\small {\large\frac{\mathrm{d}y}{\mathrm{d}x} } = {\large\frac{\mathrm{d}y}{\mathrm{d}t} } \ \div \ {\large\frac{\mathrm{d}x}{\mathrm{d}t} }}\)
\(\\[15pt]\hspace{1.2em} = \ {\small {\large \frac{ 4 \ \sin 2 t }{ 2 \ + \ 2 \ \cos 2t } } }\)
Applying double angle formula to \({\small \sin 2t \ }\) and \( \ {\small \cos 2t}\),
\(\\[1pt]\)
\(\\[15pt]\hspace{1.2em} = \ {\small {\large \frac{ 4 \ (2 \sin t \cos t) }{ 2 \ + \ 2 \ (2{\cos}^{2} t \ – \ 1) } } }\)
\(\\[15pt]\hspace{1.2em} = \ {\small {\large \frac{ 8 \ \sin t \cos t }{ 2 \ + \ 4{\cos}^{2} t \ – \ 2 } } }\)
\(\\[15pt]\hspace{1.2em} = \ {\small {\large \frac{ 8 \ \sin t \cos t }{ 4{\cos}^{2} t } } }\)
\(\\[15pt]\hspace{1.2em} = \ {\small {\large \frac{ 2 \ \sin t }{ \cos t } } }\)
\(\\[20pt]\hspace{1.2em} = \ {\small 2 \tan t }\)
\({\small\hspace{1.2em}\left(\textrm{ii}\right). \enspace }\) First, we’ll find the gradient of the tangent of the point on the curve with the perpendicular gradient formula,
\(\\[1pt]\)
\(\\[10pt]\hspace{1.2em} {\small m_{1} \times m_{2} \ = \ -1 }\)
\(\\[15pt]\hspace{3.3em} {\small m_{1} \ = \ -{\large \frac{1}{m_{2}} } }\)
\(\\[17pt]\hspace{4.8em} {\small = \ -{\large \frac{1}{2} } }\)
\(\\[15pt]\) Next, we equate \( {\small {\large\frac{\mathrm{d}y}{\mathrm{d}x} } \ = \ -{\large \frac{1}{2} }}\),
\(\\[15pt] \hspace{2.2em}{\small 2 \ \tan t \ = \ -{\large \frac{1}{2} }}\)
\(\\[15pt] \hspace{3em}{\small \tan t \ = \ -{\large \frac{1}{4} }}\)
\(\\[15pt] \hspace{4.3em}{\small t \ = \ {\tan}^{-1}\big(-{\large \frac{1}{4} }\big)}\)
\(\\[17pt] \hspace{4.3em}{\small t \ = \ -0.24498}\)
Then, we substitute \({\small t \ = \ -0.24498 }\) to find the x-coordinate of the point,
\(\\[1pt]\)
\(\\[12pt]\hspace{1.2em} {\small x \ = \ 2t \ + \ \sin 2t }\)
\(\\[15pt]\hspace{2.2em} {\small = \ 2 \ ( -0.24498 ) + \sin \ (2 \times -0.24498) }\)
\(\\[15pt]\hspace{2.2em} {\small = \ -0.961 }\)
The x-coordinate is -0.961.
\(\\[1pt]\)
\({\small 6.\enspace}\)
9709/33/M/J/20 – Paper 33 June 2020 Pure Maths 3 No 10(a), (b) \(\\[1pt]\)

\(\\[1pt]\)
A tank containing water is in the form of a hemisphere. The axis is vertical, the lowest point is \(A\) and the radius is \(r\), as shown in the diagram. The depth of water at time \(t\) is \(h\).
\(\\[1pt]\)
At time \(t = 0\) the tank is full and the depth of the water is \(r\). At this instant a tap at \(A\) is opened and water begins to flow out at a rate proportional to \(\sqrt{h}\). The tank becomes empty at time \(t = 14\).
\(\\[1pt]\)
The volume of water in the tank is \(V\) when the depth is \(h\). It is given that \( V = {\large\frac{1}{3}\pi} \big( 3r{h}^{2} \ – \ {h}^{3} \big) \).
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) Show that \(h\) and \(t\) satisfy a differential equation of the form
\(\\[1pt]\)
\(\hspace{1.2em} {\large \frac{\mathrm{d}h}{\mathrm{d}t} } \ = \ – {\large\frac{ B }{ 2r{h}^{\frac{1}{2}} \ – \ {h}^{\frac{3}{2}} } }\),
\(\\[1pt]\)
\(\hspace{1.2em}\) where \(B\) is a positive constant.
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) Solve the differential equation and obtain an expression for \(t\) in terms of \(h\) and \(r\).
Check out my solution here:
\(\\[1pt]\)
https://www.instagram.com/p/Caiu2lEs3vS/ \(\\[1pt]\)
Follow my instagram for daily updates on many more solutions on other topics too! \(\\[1pt]\)
\({\small 7.\enspace}\)
9709/33/M/J/21 – Paper 33 June 2021 Pure Maths 3 No 3(a), (b) \(\\[1pt]\)
The parametric equations of a curve are
\(\\[1pt]\)
\(\hspace{1.2em} x = \ t \ + \ln (t+2), \enspace y = \ (t \ – \ 1) { \mathrm{e} }^{-2t} \),
\(\\[1pt]\)
where \( t \ \gt \ -2 \).
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) Express \({\large\frac{\mathrm{d}y}{\mathrm{d}x} } \)in terms of \(t\), simplifying your answer.
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) Find the exact \(y\)-coordinate of the stationary point of the curve.
Check out my solution here:
\(\\[1pt]\)
https://www.instagram.com/p/Cc1meppL0CG/ \(\\[1pt]\)
Follow my instagram for daily updates on many more solutions on other topics too! \(\\[1pt]\)
\({\small 8.\enspace}\)
9709/31/M/J/21 – Paper 31 June 2021 Pure Maths 3 No 6(a), (b) \(\\[1pt]\)
The parametric equations of a curve are
\(\\[1pt]\)
\(\hspace{1.2em} x = \ln (2 \ + \ 3t), \enspace y = \ {\large\frac{t}{2 \ + \ 3t} } \).
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) Show that the gradient of the curve is always positive.
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) Find the equation of the tangent to the curve at the point where it intersects the \(y\)-axis.
Check out my solution here:
\(\\[1pt]\)
https://www.instagram.com/p/CekBuPAsmRh/ \(\\[1pt]\)
Follow my instagram for daily updates on many more solutions on other topics too! \(\\[1pt]\)
\({\small 9.\enspace}\)
9709/32/F/M/22 – Paper 32 March 2022 Pure Maths 3 No 4 \(\\[1pt]\)
The parametric equations of a curve are
\(\\[1pt]\)
\(\hspace{1.2em} x = 1 \ – \ \cos \theta, \enspace y = \cos \theta \ – \ {\large\frac{1}{4} } \cos 2\theta \).
\(\\[1pt]\)
Show that \( {\small {\large\frac{\mathrm{d}y}{\mathrm{d}x}} = -2 \ \sin^{2} \big( {\large\frac{1}{2}}\theta \big) } \).
Check out my solution here:
\(\\[1pt]\)
https://www.instagram.com/p/CniYvlVtzeL/ \(\\[1pt]\)
Follow my instagram for daily updates on many more solutions on other topics too! \(\\[1pt]\)
\({\small 10.\enspace}\)
9709/12/M/J/20 – Paper 12 June 2020 Pure Maths 1 No 3 \(\\[1pt]\)
A weather balloon in the shape of a sphere is being inflated by a pump. The volume of the balloon is increasing at a constant rate of 600 \({\small {\mathrm{cm}}^{3} }\) per second. The balloon was empty at the start of pumping.
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) Find the radius of the balloon after 30 seconds.
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) Find the rate of increase of the radius after 30 seconds.
Check out my solution here:
\(\\[1pt]\)
https://www.instagram.com/p/Cj1bUP5sbJ8/ \(\\[1pt]\)
Follow my instagram for daily updates on many more solutions on other topics too! \(\\[1pt]\)
\({\small 11.\enspace}\)
9709/12/O/N/19 – Paper 12 November 2019 Pure Maths 1 No 5 \(\\[1pt]\)
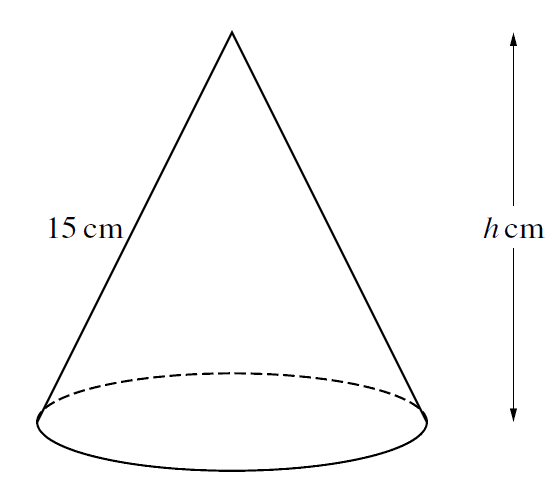
\(\\[1pt]\)
The diagram shows a solid cone which has a slant height of 15 cm and a vertical height of \({\small h}\) cm.
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(\mathrm{i}\right).\hspace{0.8em}}\) Show that the volume, \({\small V \ {\mathrm{cm}}^{3} }\), of the cone is given by \({\small V \ = \ {\large\frac{1}{3}}\pi (225h \ – \ {h}^{3}) } \).
\(\\[1pt]\)
[The volume of a cone of radius \({\small r}\) and vertical height \({\small r}\) is \({\small {\large\frac{1}{3}}\pi {r}^{2} h }\) ].
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(\mathrm{ii}\right).\hspace{0.8em}}\) Given that \({\small h}\) can vary, find the value of \({\small h}\) for which \({\small V}\) has a stationary value. Determine, showing all necessary working, the nature of this stationary value.
Check out my solution here:
\(\\[1pt]\)
https://www.instagram.com/p/CjWzXqENIa6/! \(\\[1pt]\)
Follow my instagram for daily updates on many more solutions on other topics too!\(\\[1pt]\)
PRACTICE MORE WITH THESE QUESTIONS BELOW!
\({\small 1.\enspace}\) The parametric equations of a curve are
\( x = \ \sin t \ + \cos t, \enspace y = \ {\sin}^{3}t \ + \ {\cos}^{3}t\),
where \(\frac{\pi}{4} \ \le \ t \ \le \ \frac{5\pi}{4}\)
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) Show that \({ \large\frac{\mathrm{d}y}{\mathrm{d}x}} = \ -3 \ \sin t \ \cos t \).
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) Find the gradient of the curve at the origin.
\({\small\hspace{1.2em}\left(c\right).\hspace{0.8em}}\) Find the values of t for which the gradient of the curve is 1, giving your answers correct to 2 significant figures.
\({\small 2. \enspace}\) The parametric equations of a curve are
\( x = \ a(2\theta \ – \ \sin 2\theta), \enspace y = \ a(1 \ – \ \cos 2\theta)\).
Show that \({ \large\frac{\mathrm{d}y}{\mathrm{d}x}} = \ \cot \theta \).
\({\small 3.\enspace}\) The parametric equations of a curve are
\( x = \ \ln \cos \theta, \enspace y = \ 3\theta \ – \ \tan \theta\),
where \(0 \ \le \ \theta \ \le \ \frac{1}{2}\pi\).
\({\small\hspace{1.2em}\left(\textrm{i}\right).\hspace{0.8em}}\) Express \({\small { \large\frac{\mathrm{d}y}{\mathrm{d}x}} }\) in terms of \({\small \tan \theta}\).
\({\small\hspace{1.2em}\left(\textrm{ii}\right).\hspace{0.6em}}\) Find the exact y-coordinate of the point on the curve at which the gradient of the normal is equal to 1.
\({\small 4.\enspace}\) The parametric equations of a curve are
\( x = \ {t}^{2} \ + 1, \enspace y = \ 4t \ + \ \ln \ (2t \ – \ 1)\).
\({\small\hspace{1.2em}\left(\textrm{i}\right).\hspace{0.8em}}\) Express \({\small { \large\frac{\mathrm{d}y}{\mathrm{d}x}} }\) in terms of \({\small t}\).
\({\small\hspace{1.2em}\left(\textrm{ii}\right).\hspace{0.6em}}\) Find the equation of the normal to the curve at the point where \({\small t \ = \ 1}\). Give your answer in the form ax + by + cz = 0.
\({\small 5.\enspace}\) The parametric equations of a curve are
\( x = \ t \ + \cos t, \enspace y = \ \ln \ (1 + \sin t)\),
where \(-\frac{1}{2}\pi \ \lt \ t \ \lt \ \frac{1}{2}\pi\).
\({\small\hspace{1.2em}\left(\textrm{i}\right).\hspace{0.8em}}\) Show that \({\small { \large\frac{\mathrm{d}y}{\mathrm{d}x}} \ = \ \sec t}\).
\({\small\hspace{1.2em}\left(\textrm{ii}\right).\hspace{0.6em}}\) Hence find the x-coordinates of the points on the curve at which the gradient is equal to 3. Give your answer correct to 3 significant figures.
\({\small 6.\enspace}\) A curve has parametric equations
\( x = \ {t}^{2} \ + \ 3t \ + \ 1, \enspace y = \ {t}^{4} \ + \ 1\).
The point P on the curve has parameter p. It is given that the gradient of the curve at P is 4. Show that \({\small p \ = \ \sqrt[3]{(2p \ + \ 3)} }\).
\({\small 7.\enspace}\) A curve has parametric equations
\( x = \ 1 \ + \ 2 \ \sin \theta \ \) and \( \ y = \ 4 \ + \ \sqrt{3} \ \cos \theta\).
\({\small\hspace{1.2em}\left(a\right).\hspace{0.8em}}\) Find the equations of the tangent and normal at the point P where \({\small \theta \ = \ {\large\frac{\pi}{6}} }\). Hence, find the area A of the triangle bounded by the tangent and normal at P, and the y-axis.
\({\small\hspace{1.2em}\left(b\right).\hspace{0.8em}}\) Determine the rate of change of xy at \({\small \theta \ = \ {\large\frac{\pi}{6}} }\) if x increases at a constant rate of 0.1 units/s.
\({\small 8.\enspace}\) A curve is defined parametrically by \( x \ = \ \frac{2t}{t + 1} \) and \( y \ = \ \frac{{t}^{2}}{t + 1} \).
\({\small\hspace{1.2em}\left(\textrm{i}\right).\hspace{0.8em}}\) Find the equation of the normal to the curve at the point P(1, 1/2).
\({\small\hspace{1.2em}\left(\textrm{ii}\right).\hspace{0.6em}}\) The normal at P meets the curve again at Q. Find the exact coordinates of Q.
\({\small 9.\enspace}\) A curve has parametric equations:
\( x = \ \sec (\frac{\theta}{2}), \enspace y = \ \ln \ \sec (\frac{\theta}{2})\),
where \(-\pi \ \lt \ \theta \ \lt \ \pi \).
\({\small\hspace{1.2em}\left(\textrm{i}\right).\hspace{0.8em}}\) Find the equation of the normal to the curve at the point at \({\small \theta \ = \ {\large\frac{\pi}{3}} }\).
\({\small\hspace{1.2em}\left(\textrm{ii}\right).\hspace{0.6em}}\) Determine the rate of change of x if the gradient of the curve at \({\small \theta \ = \ {\large\frac{\pi}{2}} }\) is decreasing at a rate of 0.4 units per second.
\({\small 10.\enspace}\) The parametric equations of a curve are
\( x = \ t \ + \ \ln t, \enspace y = \ t \ + \ {\textrm{e}}^{t}\) for \( t \gt 0\).
\({\small\hspace{1.2em}\left(\textrm{i}\right).\hspace{0.8em}}\) Sketch the curve, indicating clearly all intercepts and asymptotes.
\({\small\hspace{1.2em}\left(\textrm{ii}\right).\hspace{0.6em}}\) Show that, for all the points on the curve, \({\small { \large\frac{\mathrm{d}y}{\mathrm{d}x}} \ = \ { \large\frac{t(1 \ + \ {\textrm{e}}^{t})}{t \ + \ 1}} }\).
Hence, deduce that the curve does not have any turning points.
\({\small\hspace{1.2em}\left(\textrm{iii}\right).\hspace{0.4em}}\) Find, in exact form, the equation of the normal of the curve at the point where \({\small t \ = \ 1}\).
As always, if you have any particular questions to discuss, leave it in the comment section below. Cheers =) .
