Basic Algebra
Algebra is a rather new concept in primary schools but it is important to learn it early. Building a strong foundation in algebra is of paramount importance to do well in mathematics at later stages. The use of unitary/box method in problem-solving (taught at primary school) will be replaced totally by algebra (taught at secondary schools and higher). The reason is simply that it is much quicker and efficient in solving math problems.
Instead of creating a schematic of boxes as an analogy for a math problem, the value in question is being replaced by a “free variable” which then can be modified, substituted, simplified or worked out within the confined of mathematical rules and operations to arrive at the solution.
Algebra introduces the use of a “free variable”, usually denoted by a small letter. Think of this variable as something that can be replaced with any number. The order of operations (PEMDAS) for algebra still follow the same rule as before. Try some of these examples and practice more to get a good understanding of the concept!
EXAMPLE:
\({\small 2.\enspace}\) Simplify 24x + 6 – 9x – 6 + 10.
\({\small 3.\enspace}\) Luna has d watermelons. She gives 6 watermelons and packs the rest equally into 9 bags. Find the number of watermelons in each bag in terms of d.
\({\small 4.\enspace}\) Laura scored z marks in a Mathematics test. Maria scored 4 times as many marks. Nancy scored 5 more marks than Maria. Find the marks that Nancy scored in terms of z.
\({\small 5.\enspace}\) A pail and a jug contain t litres of water. The pail contains 10 times as much water as the jug. Find the amount of water in a jug in terms of t.
\({\small 6.\enspace}\) There were 45 cookies in each box. Sam purchased y boxes of cookies and gave 84 cookies to James. How many cookies did Sam have left in terms of y?
\({\small 7.\enspace}\) Mrs. Tan bought 3x packets of sugar at $8 each. She gave the cashier $100.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Find the change Mrs. Tan received in terms of x.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) If her change was $4, find the value of x.
\(\\[1pt]\)
\({\small 8.\enspace}\) Joe had $15. Ali had q times as much as Joe. Ravi had $3q more than Ali.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) How much did the 3 boys have altogether?
\({\small\hspace{1.2em}\left(b\right).\enspace}\) If q \(=\) 5, how much money did they have altogether?
\(\\[1pt]\)
\({\small 9.\enspace}\) Triangle A has a base of 6 cm and a height r cm. Triangle B has an area that is (5r + 7) \({\small \mathrm{{cm}^{2}}}\) more than area of Triangle A.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Find the area of Triangle B in terms of r.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) If r \(=\) 2, what is the area of Triangle B?
\(\\[1pt]\)
\({\small 10.\enspace}\) Ben is 15 years old. Cathy is p years older than Ben and Daniel is two times as old as Cathy.
\({\small\hspace{1.6em}\left(a\right).\enspace}\) What is the total age of Ben, Cathy and Daniel in 5 years’ time?
\({\small\hspace{1.6em}\left(b\right).\enspace}\) What is the total age of Ben, Cathy and Daniel in 10 years’ time?
\({\small\hspace{1.6em}\left(c\right).\enspace}\) If p \(=\) 3, what is the average age of the three children this year?
\(\\[1pt]\)
\({\small 11.\enspace}\) Noel had (30 + 3x) marbles. Aziz had 10 more marbles than he. Gopal had 2x fewer marbles than Aziz.
\({\small\hspace{1.6em}\left(a\right).\enspace}\) How many marbles had Azis?
\({\small\hspace{1.6em}\left(b\right).\enspace}\) How many marbles had the 3 boys altogether?
\({\small\hspace{1.6em}\left(c\right).\enspace}\) If x \(=\) 25, how many marbled had Gopal?
\(\\[1pt]\)
PRACTICE MAKES PERFECT! =)
\({\small 1.\;\left(a\right).\enspace}\) Find the value of 8m + 6m – 5m.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) What is the value of 30 – 2n if n \(=\) 6?
\({\small\hspace{1.2em}\left(c\right).\enspace}\) Bobby had m boxes of pens. There were 24 pens in each box. He sold 50 pens in all. How many pens did he have left?
\({\small 2.\;\left(a\right).\enspace}\) Simplify 8r – 5r + 6r.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) What is the value of 40 – \({\small {x}^{2}}\) if x \(=\) 5?
\({\small\hspace{1.2em}\left(c\right).\enspace}\) Marcus was given $18 per week. He spent $y per week. If y \(=\) $10, how much did he have left in 4 weeks?
\({\small 3.\;\left(a\right).\enspace}\) Find the value of \(\frac { 5m\;+\;6 }{ 4 }\) when m \(=\) 8.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) James is (15 + p) years old now. Dora is 6 years older than James. How old were they 10 years ago?
\({\small\hspace{1.2em}\left(c\right).\enspace}\) Box X is thrice as heavy as Box Y. Box Z is half as heavy as Boxes X and Y together. What is the mass of Box Z if Box Y is e kg?
\({\small 4.\;\left(a\right).\enspace}\) Find the value of 5k + 16 – 3k – 5.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) If a \(=\) 6, find the value of \({\small {a}^{3}}\) – 100.
\({\small\hspace{1.2em}\left(c\right).\enspace}\) The water from a tap flows at a rate of 6 l per minute. A tank has a capacity of 30x litres. If x \(=\) 4, how long will the tap take to fill up the tank?
\({\small 5.\enspace}\) A rope is y cm long. A steel rod is 1/3 as long as the length of the rope.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Express the length of the steel rod in terms of y.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) If a rattan cane is 15 cm long, what is the total length of the 3 items in terms of y?
\({\small\hspace{1.2em}\left(c\right).\enspace}\) If the rope is used to form a square, what is the area of the square in terms of y?
\({\small 6.\;\left(a\right).\enspace}\) Simplify 16s – 4 – 7s + 9.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) If c \(=\) 4, find the value of \(\frac{{c}^{2}\; +\; 4}{2}\) .
\({\small\hspace{1.2em}\left(c\right).\enspace}\) Meiling bought 5 blouses for $k each. She gave the cashier $50 and received $10 change. Find the value of k.
\({\small 7.\enspace}\) A rectangular photograph was pasted on a rectangular cardboard, 20 cm long and 6x cm wide, leaving a uniform margin of x cm all around it.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) What was the area of the cardboard?
\({\small\hspace{1.2em}\left(b\right).\enspace}\) What was the area of the margin if x \(=\) 2?

\({\small 8.\enspace}\) Figure 1 is a square. Its perimeter is 16y cm.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Find the length of the square.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) What is its area?
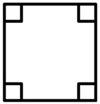
\({\small 9.\enspace}\) A square with the diagonal of 4x cm long is drawn in below figure.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Find its area in terms of x.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) If x \(=\) 4, find its area.
\({\small 10.\enspace}\) Howard, Tim and Andrew spent a sum of money. Howard and Tim each spent 25% of it.
\({\small\hspace{1.6em}\left(a\right).\enspace}\) If Andrew spent $8x, how much did Tim spend?
\({\small\hspace{1.6em}\left(b\right).\enspace}\) If Howard, Tim and Andrew decided to spend the amount of money in the ratio of 3 : 6 : 7, how much did Howard spend if x \(=\) 20?
\({\small 11.\enspace}\) A rectangular tank is 40 cm long, 30 cm wide and x cm high.
\({\small\hspace{1.6em}\left(a\right).\enspace}\) What is the volume of the tank in terms of x?
\({\small\hspace{1.6em}\left(b\right).\enspace}\) If x \(=\) 15, what is the volume of water in the tank if it is 3/4 full of water?
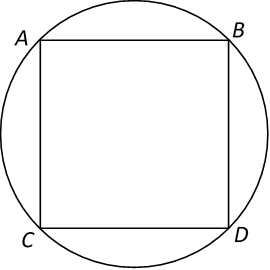
\({\small 12.\enspace}\) ABCD is a square. The radius of the circle is k cm. What is the area of the square in terms of k?
\({\small 13.\;\left(a\right).\enspace}\) John and Tracy together stood on a weighing scale and saw their total mass was 76 kg. John knew that he was p kg heavier than Tracy. What was Tracy’s mass in terms of p?
\({\small\hspace{1.6em}\left(b\right).\enspace}\) If p \(=\) 13, find the value of \({\frac{\left(3p\; -\; 9\right)}{\left(p\; +\; 7\right)}}\).
\({\small 14.\enspace}\) \(\frac{1}{3}\) of Andrew’s money is equal to \(\frac{2}{5}\) of Cecilia’s money. If Cecilia has $15y, how much do they have altogether in terms of y?
\({\small 15.\;\left(a\right).\enspace}\) Joshua travelled 5m km in 6 hours. How far could he travel in an hour if he travelled at a uniform speed?
\({\small\hspace{1.6em}\left(b\right).\enspace}\) If m \(=\) 3, how far could he travel in 2m hours?
\({\small 16.\enspace}\) Ben is (m – 5) years old now. Doreen is 8 years older than he.
\({\small\hspace{1.6em}\left(a\right).\enspace}\) What will be their total age in 12 years’ time in terms of m?
\({\small\hspace{1.6em}\left(b\right).\enspace}\) If m \(=\) 30, what was Doreen’s age 10 years ago?
\({\small 17.\enspace}\) Eddie bought 5 books at $2e each and had $5e left. How many pens could he buy with the same amount of money if each pen cost $3 each?
\({\small 18.\enspace}\) The ratio of Holy’s money to Karen’s money was 5 : 3. When Holy spent $12x, Karen had thrice as much money as she. How much did each person have at first in terms of x?
\({\small 19.\enspace}\) Billy spent \(\frac{1}{4}\) of his money on fruits and had $30m left. Then he spent the remaining amount of money on 15 similar red pens.
\({\small\hspace{1.6em}\left(a\right).\enspace}\) How much money did Billy spend on fruits? (Express the answer in terms of m.)
\({\small\hspace{1.6em}\left(b\right).\enspace}\) How many red pens could he buy with his original sum of money?
\({\small 20.\enspace}\) Mrs. Lim wants to print n numbers of name cards for her company. She has to pay a basic fee of $40 and an additional of $0.30 for each name card.
\({\small\hspace{1.6em}\left(a\right).\enspace}\) How much does she pay in term of n?
\({\small\hspace{1.6em}\left(b\right).\enspace}\) How much does she pay if she wants to print 500 name cards?
If you want to discuss any of the questions above, simply leave your comments below and I’ll get right back to it!