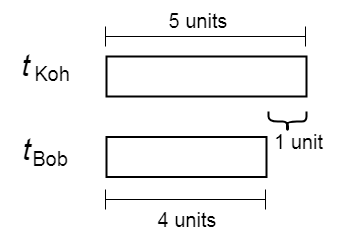The more time you spend on a journey, the more distance you will be covering. But some are slower and some are faster. To quantify this we use speed.
Speed is the rate of the distance travelled. It is the amount of distance covered over the time taken, simply a ratio of distance and time. It tells you how fast you are moving.
As an example, let’s say you travelled the first part of a journey by covering 50 km in an hour and then completed the second part of the journey by covering 60 km in two hours. What will be the average speed of the journey?
\(\\[1pt]\)
\(\\[7pt]\hspace{5em}{ s }_{ average } = \frac{50\, \mathrm{km/h}\;+\;30\, \mathrm{km/h}}{2}\)
\(\hspace{8.2em} =\) 40 km/h
\(\\[10pt]\hspace{5em} { s }_{ average } = \frac {50\; \mathrm{km}\;+ \; 60\; \mathrm{km}}{1\; \mathrm{h}\; + \; 2 \; \mathrm{h}}\)
\(\\[10pt]\hspace{8.2em} =\frac{110\; \mathrm{km}}{3\; \mathrm{h}}\)
\(\hspace{8.2em} \approx\) 36.67 km/h
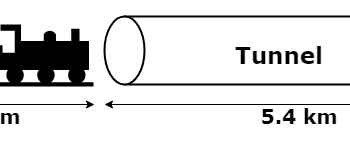
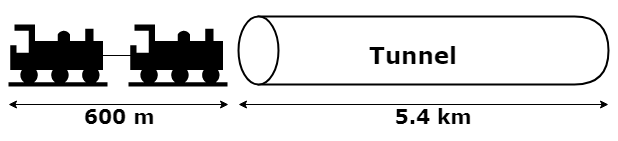
\({\small 1.\enspace}\) A train, 600 m long, enters an underground tunnel which is 5.4 km long at a speed of 120 km/h. How long will it take before the end of the train emerges from the tunnel? Give your answer in minutes.
\(\\[7pt]\hspace{2.8em}\) s \(=\) 120 km/h
The total distance is the sum of the tunnel’s and train’s length,
\(\hspace{2.8em}\) d \(=\) 5.4 km + 0.6 km (length of train in km)
\(\\[10pt]\hspace{3.5em}\) \(=\) 6 km
\(\\[10pt]\hspace{2.9em}\) t \(=\) \({\large\frac{d}{s}}\)
\(\\[10pt]\hspace{3.5em}\) \(=\) \(\frac{6\;\mathrm{km}}{120\; \mathrm{km/h}}\)
\(\\[12pt]\hspace{3.5em}\) \(=\) \(\frac{1}{20}\)h
Since 1 h \(\\[7pt]=\) 60 minutes,
\(\\[7pt]\hspace{2.9em}\) t \(=\) \(\frac{1}{20}\) \(\times\) 60
\(\\[7pt]\hspace{3.5em}\) \(=\) 3 minutes
It will take 3 minutes before the end of the train emerges from the tunnel.
\(\\[1pt]\)
\({\small 2.\enspace}\) Cecilia and Janet ran in a race. When Janet completed the run in 30 minutes, Cecilia had only run \(\frac{5}{9}\) of the distance. Cecilia’s average speed for the race was 60 m/min less than Janet’s.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Find the distance of the race.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) What was Cecilia’s speed in m/min?
In this question, we will use the concept of “Ratio Multiplication/Division” and also the unitary/box method. Let’s look at how this is done closely:
\(\\[1pt]\)
\({\small\hspace{1.2em}\left(a\right).\enspace}\) \({t}_{\mathrm{Janet}}\; :\; {t}_{\mathrm{Cecilia}}\) \(=\) 30 mins : 30 mins
\(\hspace{9.6em}\) \(=\) 1 : 1
\(\\[7pt]\hspace{3.3em} {d}_{\mathrm{Janet}}\; :\; {d}_{\mathrm{Cecilia}}\) \(=\) 9 : 5
\(\\[10pt]\hspace{3.3em} {s}_{\mathrm{Janet}}\; :\; {s}_{\mathrm{Cecilia}}\) \(=\) \(\frac{9}{1}\) : \(\frac{5}{1}\)
\(\hspace{9.6em}\) \(=\) 9 : 5
\(\\[1pt]\)
Notice how we can use the formula,
s \(=\) \(\frac{d}{t}\) by dividing the known
ratio values although
the exact values may not be known beforehand. This is an example of “Ratio Division”.
\(\\[1pt]\)

\(\\[1pt]\)
\(\hspace{2.8em}\) 4 units \(=\) 60 m/min
\(\\[7pt]\hspace{2.8em}\) 1 unit \(=\) \(\frac{60}{4}\)
\(\\[10pt]\hspace{5.5em}\) \(=\) 15 m/min
\(\hspace{2.8em} {s}_{\mathrm{Janet}}\) \(=\) 9 units \(\times\) 15 m/min
\(\\[10pt]\hspace{5.5em}\) \(=\) 135 m/min
\(\hspace{2.8em} {d}_{\mathrm{Janet}}\) \(=\) \({s}_{\mathrm{Janet}} \times {t}_{\mathrm{Janet}}\)
\(\hspace{5.5em}\) \(=\) 135 \(\times\) 30
\(\\[7pt]\hspace{5.5em}\) \(=\) 4050 m
The distance of the race is 4050 m. \(\\[1pt]\)
\({\small\hspace{1.2em}\left(b\right).\enspace}\) \({s}_{\mathrm{Cecilia}}\) \(=\) 5 units \(\times\) 15 m/min
\(\\[7pt]\hspace{6.4em}\) \(=\) 75 m/min
Cecilia’s speed was 75 m/min. \(\\[1pt]\)
\({\small 3.\enspace}\) Raju set off from his house at 1 p.m. and travelled at a uniform speed of 75 km/h towards Gopal’s house. He increased his speed to 90 km/h at 3 p.m. and reached Gopal’s house at 6 p.m.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Find the distance between Raju’s and Gopal’s houses.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) Find the average speed of the whole journey.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) d \(=\) (75 km/h \(\times\) 2 h) + (90 km/h \(\times\) 3 h)
\(\\[7pt]\hspace{3.9em}\) \(=\) 420 km
The distance between Raju’s and Gopal’s houses was 420 km.
\(\\[1pt]\)
\(\\[7pt]{\small\hspace{1.2em}\left(b\right).\enspace}\) \({s}_{\mathrm{average}}\) \(=\) \(\frac{420\; \mathrm{km}}{5\; \mathrm{h}}\)
\(\\[7pt]\hspace{6.2em}\) \(=\) 84 km/h
The average speed of the whole journey was 84 km/h.
\(\\[1pt]\)
\({\small 4.\enspace}\) At 10.00 a.m., Mr. Koh’s car passed a certain point, A, travelling at an average speed of 80 km/h. At 11.30 a.m., Mr. Bob’s car started off from point A at an average speed of 100 km/h in pursuit of Mr. Koh’s car.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) At what time did Mr. Bob’s car overtake Mr. Koh’s car?
\({\small\hspace{1.2em}\left(b\right).\enspace}\) How far was Mr. Bob’s car from point A when it overtook Mr. Koh’s car?
This is another example of “Ratio Division” problem.
\(\\[1pt]\)
\(\\[7pt]\hspace{1.2em}\left(a\right).\enspace {d}_{\mathrm{Koh}}\; :\; {d}_{\mathrm{Bob}}\) \(=\) 1 : 1
\(\\[7pt]\hspace{3.6em} {s}_{\mathrm{Koh}}\; :\; {s}_{\mathrm{Bob}}\) \(=\) 80 \(\frac{\mathrm{km}}{\mathrm{h}}\) : 100 \(\frac{\mathrm{km}}{\mathrm{h}}\)
\(\\[7pt]\hspace{9.5em}\) \(=\) 4 : 5
\(\\[7pt]\hspace{3.7em} {t}_{\mathrm{Koh}}\; :\; {t}_{\mathrm{Bob}}\) \(=\) \(\frac{1}{4}\) : \(\frac{1}{5}\)
\(\hspace{9.4em}\) \(=\) 5 : 4
\(\\[1pt]\)
Notice how we use the formula,
t \(=\) \(\frac{d}{s}\) to get the ratio of \({t}_{\mathrm{Koh}}\) and \({t}_{\mathrm{Bob}}\).
\(\\[1pt]\)
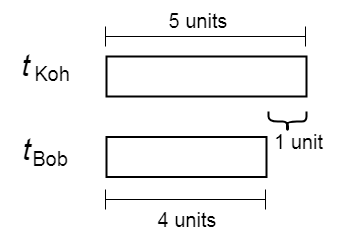
\(\\[1pt]\)
\(\\[7pt]\hspace{2.8em}\) 1 unit \(=\) \(1\frac{1}{2}\) h
\(\\[7pt]\hspace{3.3em} {t}_{\mathrm{Bob}}\) \(=\) 11.30 a.m. + 4 units \(\times\;1\frac{1}{2}\) h
\(\hspace{5em}\) \(=\) 11.30 a.m. + 6 h
\(\\[7pt]\hspace{5em}\) \(=\) 5.30 p.m.
Mr. Bob’s car overtook Mr. Koh’s car at 5.30 p.m. \(\\[1pt]\)
\(\\[7pt]{\small\hspace{1.2em}\left(b\right).\enspace}\) \({d}_{\mathrm{Bob}}\) \(=\) \({s}_{\mathrm{Bob}}\;\times{t}_{\mathrm{Bob}}\)
\(\hspace{5em}\) \(=\) 100 km/h \(\times\) 6 h
\(\\[7pt]\hspace{5em}\) \(=\) 600 km
Mr. Bob’s car travelled 600 km from point A when it overtook Mr. Koh’s car. \(\\[1pt]\)
\({\small 5.\enspace}\) Alicia left Town X and drove to Town Z. After travelling \(\frac{1}{4}\) of the journey at an average speed of 72 km/h for 40 minutes, she stopped at Town Y to have a break for 20 minutes. Then she carried on with the journey at an average speed of 80 km/h. She reached Town Z at 3.45 p.m.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) What was the distance between Town Y and Town Z?
\({\small\hspace{1.2em}\left(b\right).\enspace}\) What was the time when Alicia left Town X?
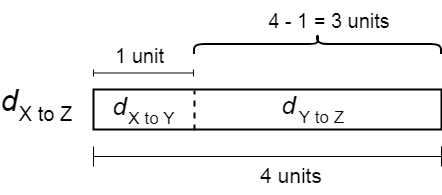
\(\\[1pt]\)
\(\\[7pt]{\small\hspace{1.2em}\left(a\right).\enspace}\) \({d}_{\mathrm{X to Y}}\) \(=\) \({s}_{\mathrm{X to Y}}\;\times{t}_{\mathrm{X to Y}}\)
\(\\[7pt]\hspace{5.7em}\) \(=\) 72 km/h \(\times\) \(\frac{40}{60}\) h
\(\hspace{5.7em}\) \(=\) 48 km
\(\\[7pt]\hspace{3.2em}\) \({d}_{\mathrm{Y to Z}}\) \(=\) 3 units \(\times\) 48 km
\(\\[7pt]\hspace{5.7em}\) \(=\) 144 km
The distance between Town Y and Town Z was 144 km. \(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.2em}\left(b\right).\enspace}\) \({t}_{\mathrm{Y to Z}}\) \(=\) \({\large\frac{{d}_{\mathrm{Y to Z}}}{{s}_{\mathrm{Y to Z}}}}\)
\(\\[10pt]\hspace{5.4em}\) \(=\) \(\frac{144\;\mathrm{km}}{80\; \mathrm{km/h}}\)
\(\\[7pt]\\[10pt]\hspace{5.4em}\) \(=\) \(1\frac{4}{5}\) h
The total time taken for the whole journey from Town X to Town Y was,
\(\\[10pt]\hspace{3em}\) \(=\) \(1\frac{4}{5}\) h + \(\frac{20}{60}\) h + \(\frac{40}{60}\) h
\(\\[7pt]\\[10pt]\hspace{3em}\) \(=\) \(2\frac{4}{5}\) h
The time when Alicia left Town X was,
\(\\[7pt]\hspace{3em}\) \(=\) 3.45 p.m – \(2\frac{4}{5}\) h
\(\hspace{3em}\) \(=\) 12.57 p.m. \(\\[1pt]\)
\({\small 6.\enspace}\) A car and a van were travelling from Town A to Town B which were 480 km apart. The van left Town A at 9.30 a.m. and drove towards Town B at an average speed of 60 km/h. The car set off 2 hours later than the van but it arrived at Town B 1 hour earlier.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) At what time did the car arrive at Town B?
\({\small\hspace{1.2em}\left(b\right).\enspace}\) How much faster was the car travelling than the van per hour?
\(\\[10pt]{\small\hspace{1.2em}\left(a\right).\enspace}\) \({t}_{\mathrm{van}}\) \(=\) \({\large\frac{{d}_{\mathrm{van}}}{{s}_{\mathrm{van}}}}\)
\(\\[10pt]\hspace{4.8em}\) \(=\) \(\frac{480\;\mathrm{km}}{60\; \mathrm{km/h}}\)
\(\\[10pt]\hspace{4.8em}\) \(=\) 8 h
\(\hspace{3.3em}\) \({t}_{\mathrm{car}}\) \(=\) 8 – 2 – 1
\(\\[7pt]\hspace{4.8em}\) \(=\) 5 h
The car arrived at Town B at,
\(\hspace{4.8em}\) = 9.30 a.m. + 2 h + 5 h
\(\hspace{4.8em}\) = 4.30 p.m.
\(\\[1pt]\)
\(\\[10pt]{\small\hspace{1.2em}\left(b\right).\enspace}\) \({v}_{\mathrm{car}}\) \(=\) \({\large\frac{{d}_{\mathrm{car}}}{{t}_{\mathrm{car}}}}\)
\(\\[10pt]\hspace{4.8em}\) \(=\) \(\frac{480\;\mathrm{km}}{5\; \mathrm{h}}\)
\(\\[7pt]\hspace{4.8em}\) \(=\) 96 km/h
The difference in car’s speed and van’s speed,
\(\hspace{4.8em}\) \(=\) 96 km/h – 60 km/h
\(\\[7pt]\hspace{4.8em}\) \(=\) 36 km/h
The car was travelling 36 km faster than the van per hour.
\(\\[1pt]\)
\({\small 7.\enspace}\) Tom and Jerry started travelling from Point X on a road but in the opposite direction. After 2 hours, they were 292 km apart. Jerry’s average speed was 10 km/h slower than Tom’s. What was Jerry’s average speed?
Since Jerry’s average speed was 10 km/h slower than Tom’s, the difference in the distance travelled between Tom and Jerry was,
\(\\[1pt]\)
\(\hspace{3.3em}\) \({\small\Delta d}\) \(=\) \({\small\Delta v\; \times\; t}\)
\(\hspace{4.6em}\) \(=\) 10 km/h \(\times\) 2 h
\(\\[7pt]\hspace{4.6em}\) \(=\) 20 km
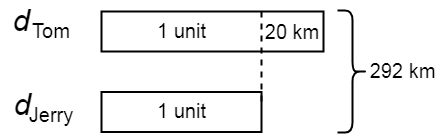
\(\\[1pt]\)
\(\hspace{3em}\) 2 units \(=\) 292 km – 20 km
\(\hspace{5.7em}\) \(=\) 272 km
\(\\[7pt]\hspace{3.4em}\) 1 unit \(=\) \(\frac{272\; \mathrm{km}}{2}\)
\(\\[7pt]\hspace{5.7em}\) \(=\) 136 km
\(\hspace{3.3em}\) \({d}_{\mathrm{Jerry}}\) \(=\) 1 unit
\(\\[10pt]\hspace{5.7em}\) \(=\) 136 km
\(\\[12pt]\hspace{3.3em}\) \({s}_{\mathrm{Jerry}}\) \(=\) \({\large\frac{{d}_{\mathrm{Jerry}}}{{t}_{\mathrm{Jerry}}}}\)
\(\\[7pt]\hspace{5.7em}\) \(=\) \(\frac{136\; \mathrm{km}}{2\; \mathrm{h}}\)
\(\\[7pt]\hspace{5.7em}\) \(=\) 68 km/h
Jerry’s average speed was 68 km/h. \(\\[1pt]\)
\({\small 8.\enspace}\) Louis and Edmund left Town B at the same time, heading in the opposite direction. Louis headed for Town C while Edmund left for Town A. The speed of Edmund was 12 km/h faster than that of Louis. After 30 minutes, Louis had completed \(\frac{2}{3}\) of his journey while Edmund had completed \(\frac{1}{4}\) of his journey. They were also 90 km apart.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Calculate the speed of Louis.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) How far was Edmund from Town A when Louis reached his destination?
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Since Edmund was 12 km/h faster than that of Louis, after 30 minutes, the difference in the distance travelled between Edmund and Louis was,
\(\\[1pt]\)
\(\hspace{3.3em}\) \({\small\Delta d}\) \(=\) \({\small\Delta v\; \times\; t}\)
\(\\[7pt]\hspace{4.6em}\) \(=\) 12 km/h \(\times\) \(\frac{30}{60}\) h
\(\hspace{4.6em}\) \(=\) 6 km
\(\\[1pt]\)
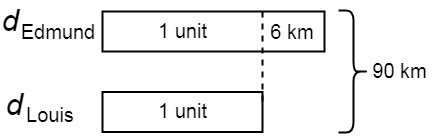
\(\\[1pt]\)
\(\hspace{3em}\) 2 units \(=\) 90 km – 6 km
\(\\[7pt]\hspace{5.7em}\) \(=\) 84 km
\(\\[7pt]\hspace{3.4em}\) 1 unit \(=\) \(\frac{84\; \mathrm{km}}{2}\)
\(\\[7pt]\hspace{5.7em}\) \(=\) 42 km
\(\hspace{3.3em}\) \({d}_{\mathrm{Louis}}\) \(=\) 1 unit
\(\\[15pt]\hspace{5.7em}\) \(=\) 42 km
\(\\[12pt]\hspace{3.3em}\) \({s}_{\mathrm{Louis}}\) \(=\) \({\large\frac{{d}_{\mathrm{Louis}}}{{t}_{\mathrm{Louis}}}}\)
\(\\[10pt]\hspace{5.7em}\) \(=\) \(\frac{42\; \mathrm{km}}{(30/60)\; \mathrm{h}}\)
\(\\[7pt]\hspace{5.7em}\) \(=\) 84 km/h
Louis’ speed was 84 km/h. \(\\[1pt]\)
\({\small\hspace{1.2em}\left(b\right).\enspace}\) The solution to this part is quite challenging. Let’s break it into few steps:
Step 1:\(\enspace\) Find the distance travelled by Edmund after 30 minutes and the speed of Edmund. \(\\[1pt]\)
\(\hspace{3.3em}\) \({d}_{\mathrm{Edmund}}\) \(=\) 1 unit + 6 km
\(\hspace{6.6em}\) \(=\) 42 km + 6 km
\(\\[10pt]\hspace{6.6em}\) \(=\) 48 km
\(\hspace{3.3em}\) \({s}_{\mathrm{Edmund}}\) \(=\) 84 km/h + 12 km/h
\(\hspace{6.6em}\) \(=\) 96 km/h
\(\\[1pt]\)
Step 2:\(\enspace\) Find the total distance travelled by Edmund from Town B to Town A. \(\\[1pt]\)
\(\hspace{3.3em}\) \({d}_{\mathrm{Edmund(total)}}\) \(=\) 4 units \(\times\) 48 km
\(\\[7pt]\hspace{8.7em}\) \(=\) 192 km
We need Edmund’s total distance to find how far Edmund was from Town A.
\(\\[1pt]\)
Step 3:\(\enspace\) Find the total distance travelled by Louis from Town B to Town C. \(\\[1pt]\)
\(\\[7pt]\hspace{3em}\) 2 units \(=\) 42 km
\(\\[7pt]\hspace{3.3em}\) 1 unit \(\; =\) \(\frac{42\; \mathrm{km}}{2}\)
\(\hspace{5.8em}\) \(=\) 21 km
\(\hspace{3.3em}\) \({d}_{\mathrm{Louis(total)}}\) \(=\) 3 units \(\times\) 21 km
\(\hspace{7.8em}\) \(=\) 66 km
\(\\[1pt]\)
Step 4:\(\enspace\) Find the time taken by Louis to travel from Town B to Town C. \(\\[1pt]\)
\(\\[15pt]\hspace{3.3em}\) \({t}_{\mathrm{Louis(total)}}\) \(=\) \({\large\frac{{d}_{\mathrm{Louis(total)}}}{{s}_{\mathrm{Louis}}}}\)
\(\\[12pt]\hspace{7.6em}\) \(=\) \(\frac{66\; \mathrm{km}}{84 \mathrm{km/h}}\)
\(\hspace{7.6em}\) \(=\) \(\frac{3}{4}\) h
\(\\[1pt]\)
Step 5:\(\enspace\) Find the distance Edmund had travelled when Louis reached his destination. \(\\[1pt]\)
\(\hspace{3.3em}\) \({\small d}\) \(=\)
v \(\times\)
t \(\\[7pt]\hspace{3.9em}\) \(=\) 96 km/h \(\times\) \(\frac{3}{4}\) h
\(\hspace{3.9em}\) \(=\) 72 km
\(\\[1pt]\)
Step 6:\(\enspace\) Get the final answer by subtracting the distance found in Step 5 from the total distance to Town A. \(\\[1pt]\)
Edmund’s distance from Town A,
\(\hspace{4.5em}\) \(=\) 192 km – 72 km
\(\\[7pt]\hspace{4.5em}\) \(=\) 120 km
Edmund was 120 km from Town A when Louis reached his destination.\({\small 1.\enspace}\) A man jogs around his estate for 45 minutes at 8 km/h. Find the distance the man jogged.
\({\small 2.\enspace}\) Dennis rowed a boat at a speed of 18 m/min. After every 3 minutes of rowing, he rested for 2 minutes. At this speed, how long would he take to reach his destination which is at 126 m ahead?
\({\small 3.\enspace}\) A train took 8 hours to travel from Town X to Town Y at an average speed of 72 km/h. An express train took only 6 hours for the same journey. What was the average speed of the express train?
\({\small 4.\enspace}\) Belinda travelled at 80 km/h for the first \(\frac{4}{9}\) of her journey. She then completed the remaining journey in 40 minutes at 90 km/h. How long did she take to complete the whole journey? Express your answer in hours and minutes.
\({\small 5.\enspace}\) Richard and Karen had a car race. Richard drove at an average speed of 56 km/h and Karen drove at an average speed of 77 km/h. If Richard started 1 h 30 min earlier than Karen, how long would she take to catch up with Richard?
\({\small 6.\enspace}\) Macy travelled at 72 km/h for \(\frac{5}{9}\) of her journey. She took a 48 min break and continued travelling another 1.5 hours of the remaining journey at 96 km/h.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) Find the distance of her journey.
\({\small\hspace{1.2em}\left(b\right).\enspace}\) What was the average speed of her journey?
\({\small 7.\enspace}\) Mr. Tan left Town A and reached Town B by car in 6 hours. Cecilia left Town A later and was 60 km from Town B when Mr. Tan reached Town B. If the distance between Town A and Town B was 420 km and the average travelling speed of Cecilia was 20 km/h faster than Mr. Tan,
\({\small\hspace{1.2em}\left(a\right).\enspace}\) how much later did Cecilia leave Town A than Mr. Tan?
\({\small\hspace{1.2em}\left(b\right).\enspace}\) how many more minutes did Cecilia take to travel to reach Town B than Mr. Tan?
\({\small 8.\enspace}\) Amber and Gina are sisters staying together. At 2.30 p.m., Amber travelled from her home to a jetty at a speed of 54 km/h. After some time, Gina left her home for the jetty travelling at a speed of 72 km/h. At 5.10 p.m., both Gina and Amber reached the jetty.
\({\small\hspace{1.2em}\left(a\right).\enspace}\) At what time did Gina leave her home?
\({\small\hspace{1.2em}\left(b\right).\enspace}\) Find the distance Amber drove from her home to the jetty.
\({\small 9.\enspace}\) Mr. Chia, on his way from his house to Town Halong, after covering \(\frac{3}{8}\) of his journey, passed a lorry which was travelling at an average speed of 80 km/h. When Mr. Chia reached his destination 4 hours later, the lorry was still 60 km away from Town Halong. If the lorry had started from Town Bay which was 48 km away from Mr. Chia’s house, how long did the lorry take to travel from Town Bay to Town Halong?
\({\small 10.\enspace}\) Two boys were competing in a race around their school’s 400 m track. From the same starting point, Mathew ran at a speed of 1.2 m/s and Thomas ran at a speed of 1.6 m/s. How long, in seconds, did Thomas take to pass Mathew twice?
\(\\[1pt]\)
As always, leave your comments for any questions or discussion. Cheers =) .